데이터 전처리 Part 2 - 변수 다루기
변수는 어떻게 다뤄야 할까?
1.변수의 종류 Recap
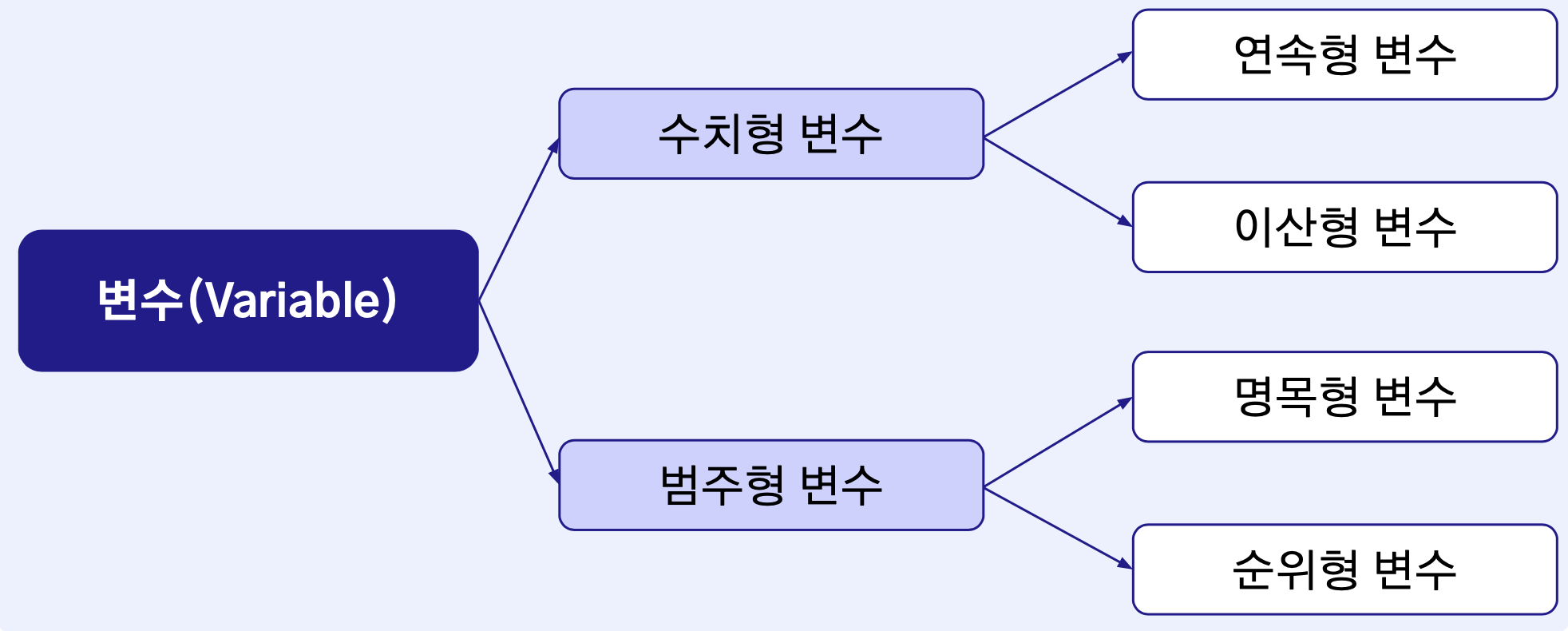
이전에 정리한 내용에서는 정형 데이터에서 변수는 그림과 같이 구분할 수 있다고 했었다.
- 변수는 수치형 값이면서 수학적 연산이 가능한가에 따라
수치형 변수와범주형 변수로 구분. - 연속형 변수는 값이 연속적인가 이산적인가에 따라
연속형 변수와이산형 변수로 구분. - 범주형 변수는 범주에 순위가 적용되었는가에 따라
명목형 변수와순위형 변수로 구분.
이번 글에서는 이렇게 다양한 변수들을 어떻게 다루어야할지 정리할 것인데, 이전 내용에서 마지막 부분인 “이상치 변환”에서 다루고자 했던 변환(Transformation)이 등장한다.
2.연속형 변수
2-1.변환
1.로그 변환
로그 변환은 변수 값들에 로그함수(log)를 적용하는 것으로 Right-Skewed인 분포를 정규분포에 가깝게 변환시켜준다. 여기서 정규분포에 가까워지게 만드는 목적은 다음과 같은 이유가 있다.
- 많은 통계 기법과 검정은 데이터가 정규분포를 따른다는 가정을 기반으로 한다. 즉, 통계적 분석을 할 때 정규분포에 가까워지면 해석도 용이하고 결과가 신뢰성이 높아진다.
- 대부분의 머신러닝 알고리즘(모델)은 데이터의 분포에 민감하다. 따라서 정규분포에 가까운 데이터는 모델의 성능을 향상시킬 수 있다.
- 정규분포는 평균과 표준편차를 기준으로 데이터의 위치를 이해하는데 효과적이다.
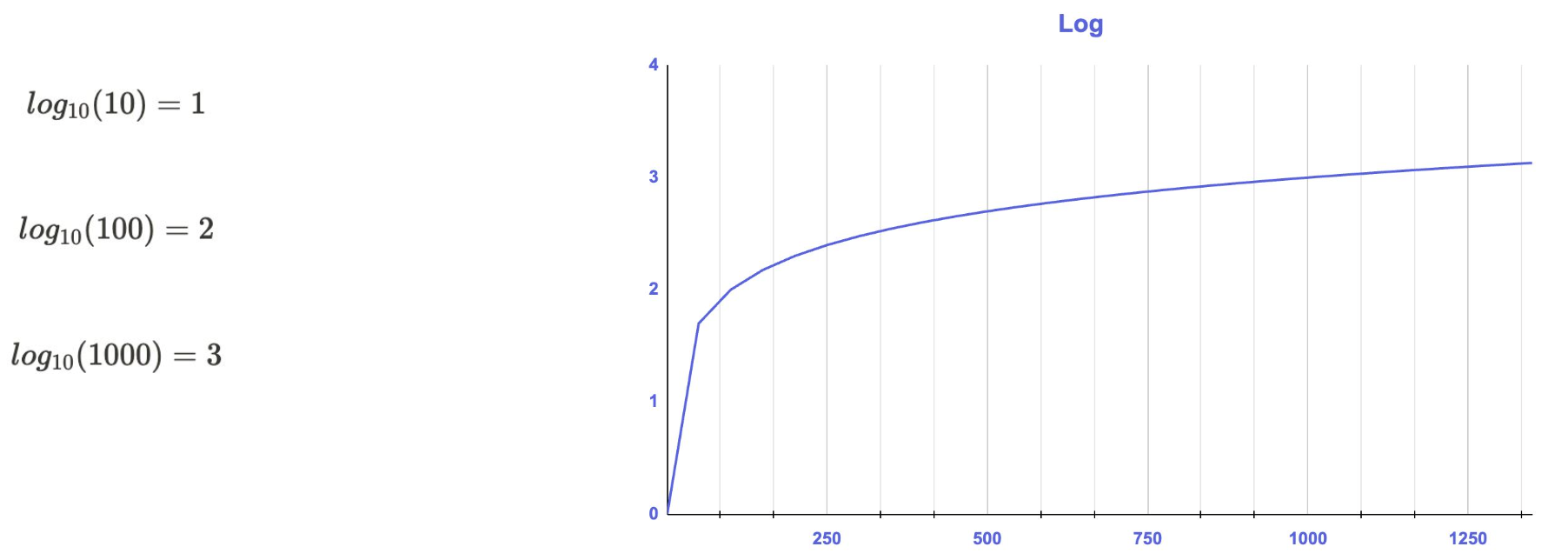
그림에서 보이듯 로그 변환은 입력 x의 값이 크면 클수록 감소시키는 폭이 굉장히 커진다. 즉, 큰 값일수록 더 작게 만들어 데이터들의 편차가 줄어드는 효과가 있으며 이로 인해 Right-Skewed 분포가 완화되는 것이다. 이를 다르게 해석하면 값이 비정상적으로 큰 이상치를 정상적인 데이터 분포로 끌고 오는 효과가 있어 이상치 처리도 가능하다. 하지만 로그의 특성상 입력이 0이거나 음수인 Left-Skewed 분포인 경우 적용이 불가능하다. 따라서 해당 변수의 분포를 먼저 확인하고 $ x \geq 0 $인 경우에만 로그 변환을 활용하자.
참고로 numpy에는 log1p라는 함수가 있는데, 이 함수는 $log(x + 1)$ 을 계산하기 때문에 $x=0 \rightarrow log(0 + 1)=0$을 처리할 수 있다.
2.제곱근 변환
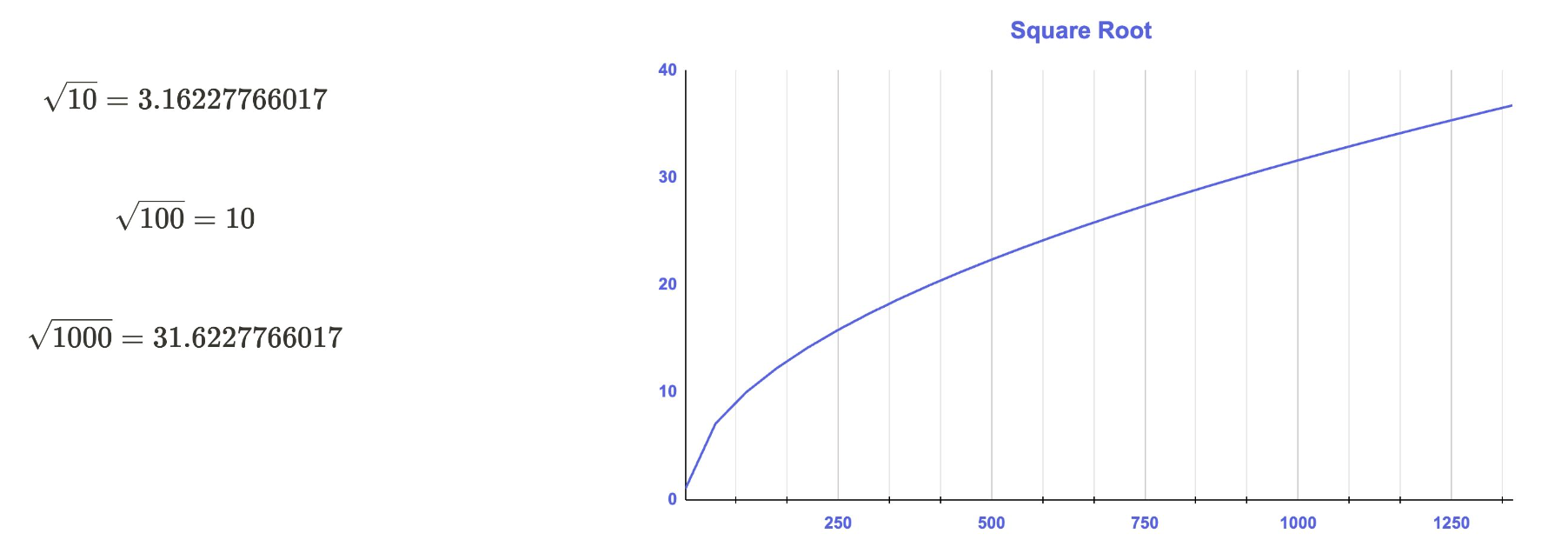
제곱근 변환은 로그 대신 제곱근(Square root)를 적용하는 것으로 로그 함수처럼 입력값을 줄이며 그로인해 발생하는 효과 역시 비슷하다. 다만 로그보다는 입력값을 줄이는 정도가 약하기 때문에 Right-Skewed의 정도가 강한 경우엔 로그 변환을, 약한 경우 제곱근 변환을 사용한다. 로그와 마찬가지로 0과 음수를 처리할 수 없기 때문에 Left-Skewed 분포에서는 적용이 불가능하다.
3.거듭제곱 변환
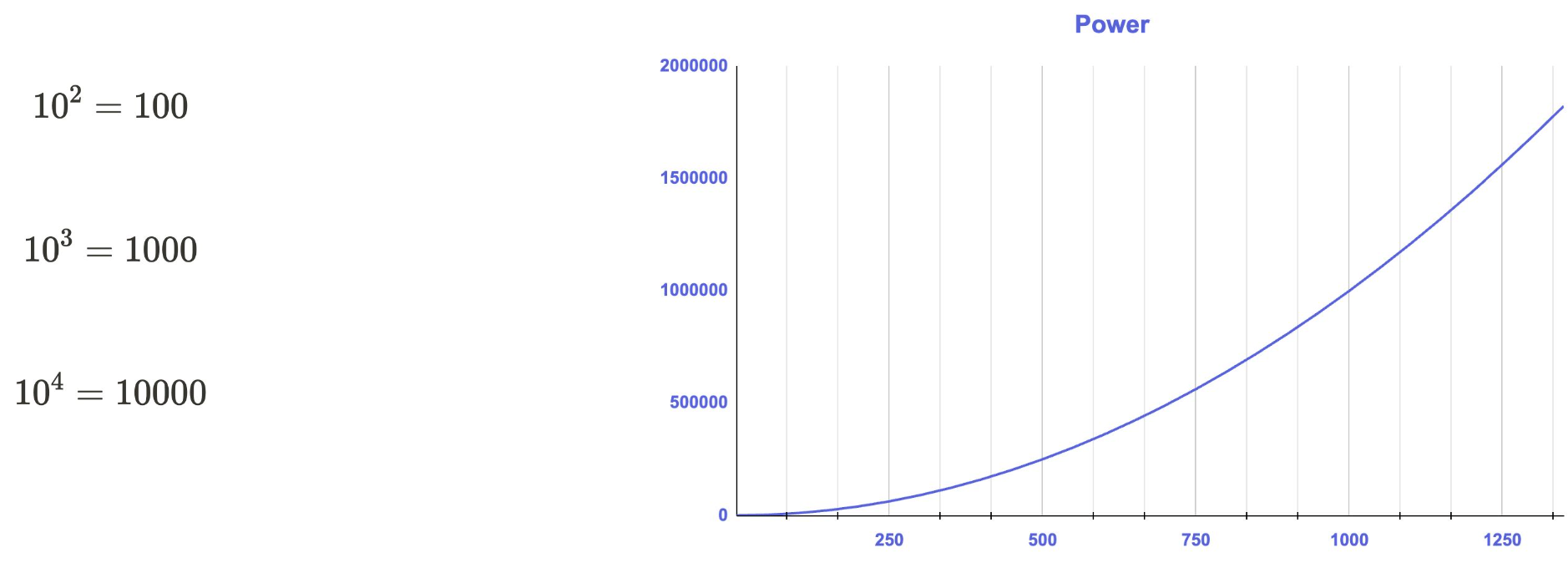
변수값에 거듭제곱을 적용하는 변환으로 입력값이 크면 클수록 더 큰 값으로 변환시킨다.
4. Box-Cox 변환
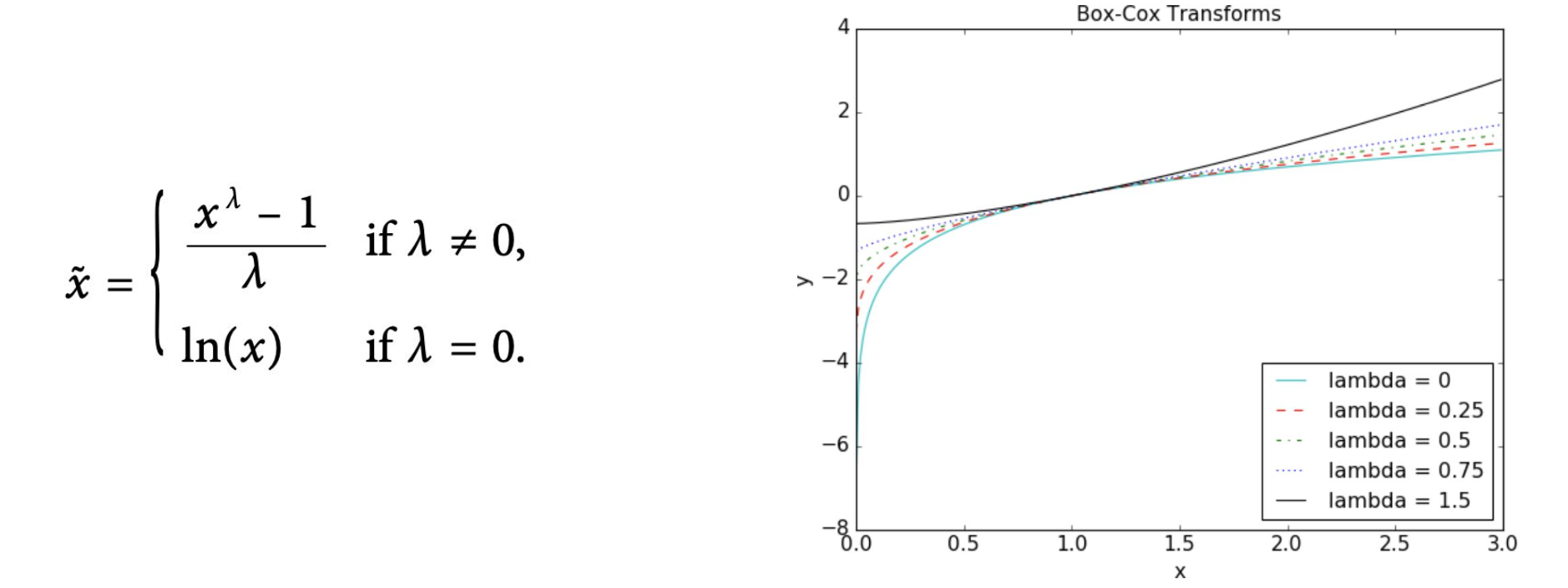
수식에서 보이듯 lambda($\lambda$) 파라미터가 존재하며 어떻게 값을 설정하는가에 따라 변환이 달라진다. 따라서 여러 가지 값을 적용해보고 목적에 알맞는 값을 찾는 것이 중요하다.
- $\lambda=0$ : 로그 변환.
- $\lambda > 0$ : 거듭제곱 변환.
- $\lambda < 0$ 거듭제곱의 역수 변환.
2-2. 스케일링
스케일링은 각각의 변수들이
댓글남기기