데이터 전처리 Part 1 - 결측치와 이상치
결측치와 이상치란 무엇일까?
1.데이터 전처리와 좋은 데이터
머신러닝에서 좋은 데이터는 데이터 샘플들의 다양성이 높으면서 노이즈가 적은 것을 말한다.
- 아무리 데이터셋의 규모가 크다고 하더라도 이를 구성하는 데이터 샘플이 한쪽으로 편향된 경향을 보인다면 학습을 잘했어도 편향적인 결과를 출력하게 되어 일반화 성능이 낮다.
- 데이터가 노이즈를 내재하고 있는 경우엔 모델이 Global Optima에 도달할 수 없다. 여기서 말하는 노이즈란 크게 결측치, 이상치, 잘못된 라벨(label), 중복 데이터 샘플, 도메인을 벗어난 샘플로 구분할 수 있다.
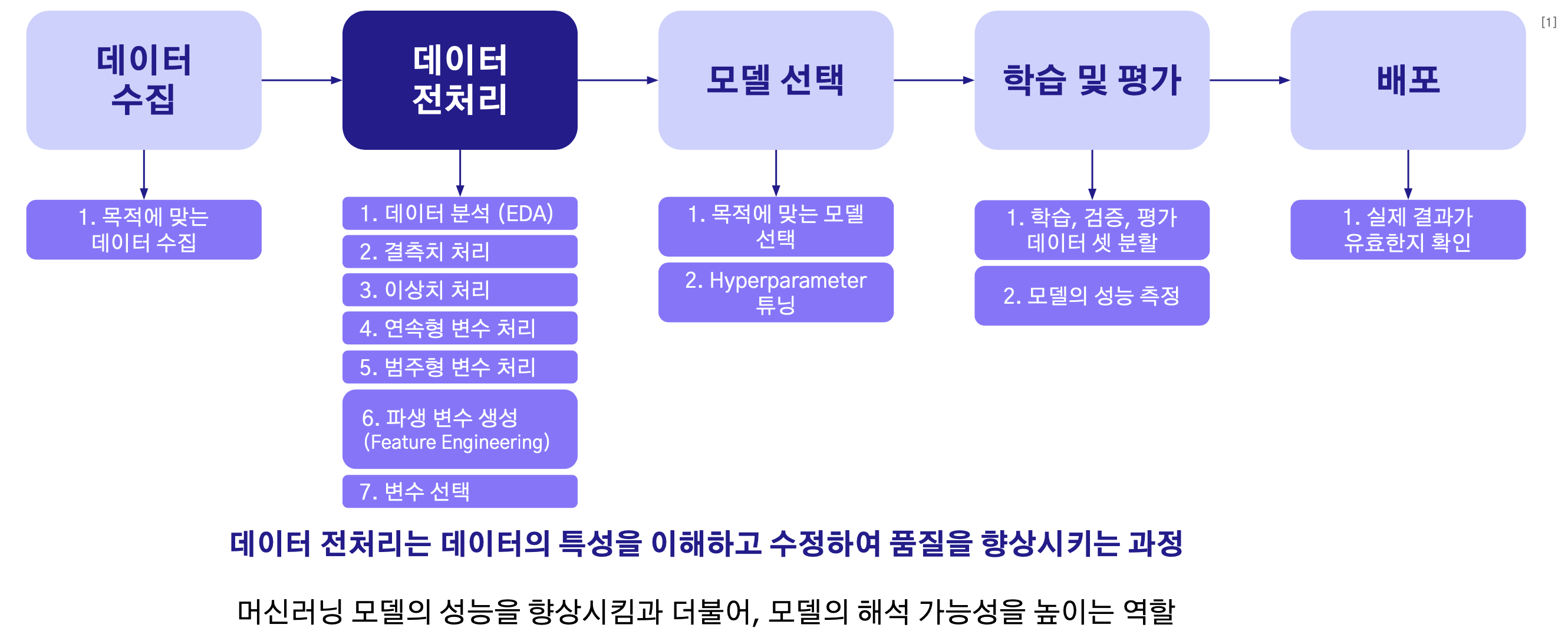
이처럼 데이터셋은 다양한 문제들을 보유하고 있을 수 있는데 이를 해결하는 단계가 바로 데이터 전처리단계이다. 데이터 전처리 단계는 탐색적 데이터 탐색(EDA) 단계를 기반으로 수행되는데, 쉽게 말하면 데이터를 탐색하는 과정에서 결측치, 이상치 그리고 편향성 등등 모델 학습 및 일반화 성능에서 문제가 될 수 있는 부분들을 사전에 처리하는 과정이라 할 수 있겠다.
그렇다면 우리가 탐색과정에서 찾아내야할 문제점이 무엇이 있는지 그리고 이들은 어떻게 처리를 해야할지 하나하나 짚어보도록 하자.
2.변수(Variable, Feature)
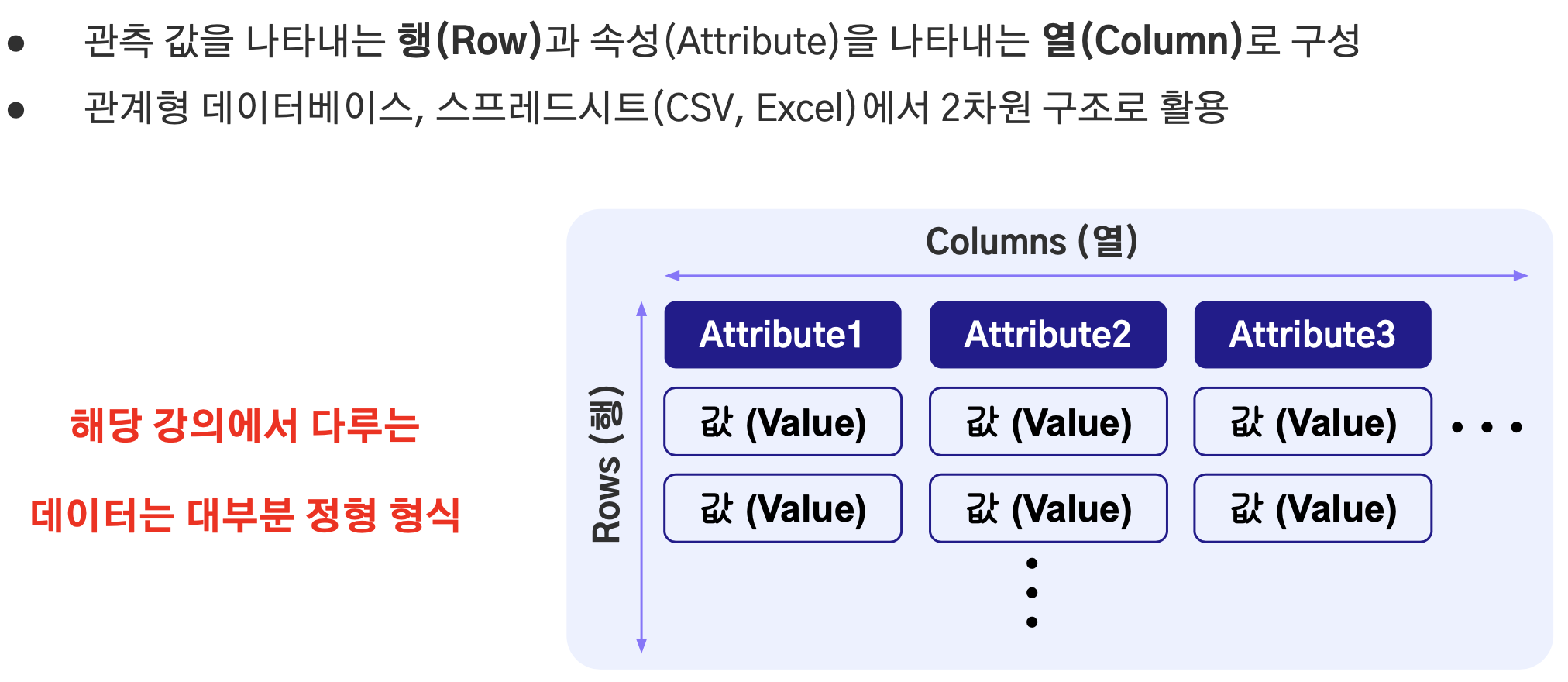
머신러닝 모델은 일반적으로 정형 데이터로 학습되는데 정형 데이터는 우리가 일상에서 흔히 사용하는 엑셀이나 csv와 같은 테이블로 구성된 데이터로 보면 된다. 즉, 관측된 값을 행(Row)으로, 속성(Attribute)를 열(Column)으로 구성되며 각각의 열을 변수, Variable, Feature로 해석한다.
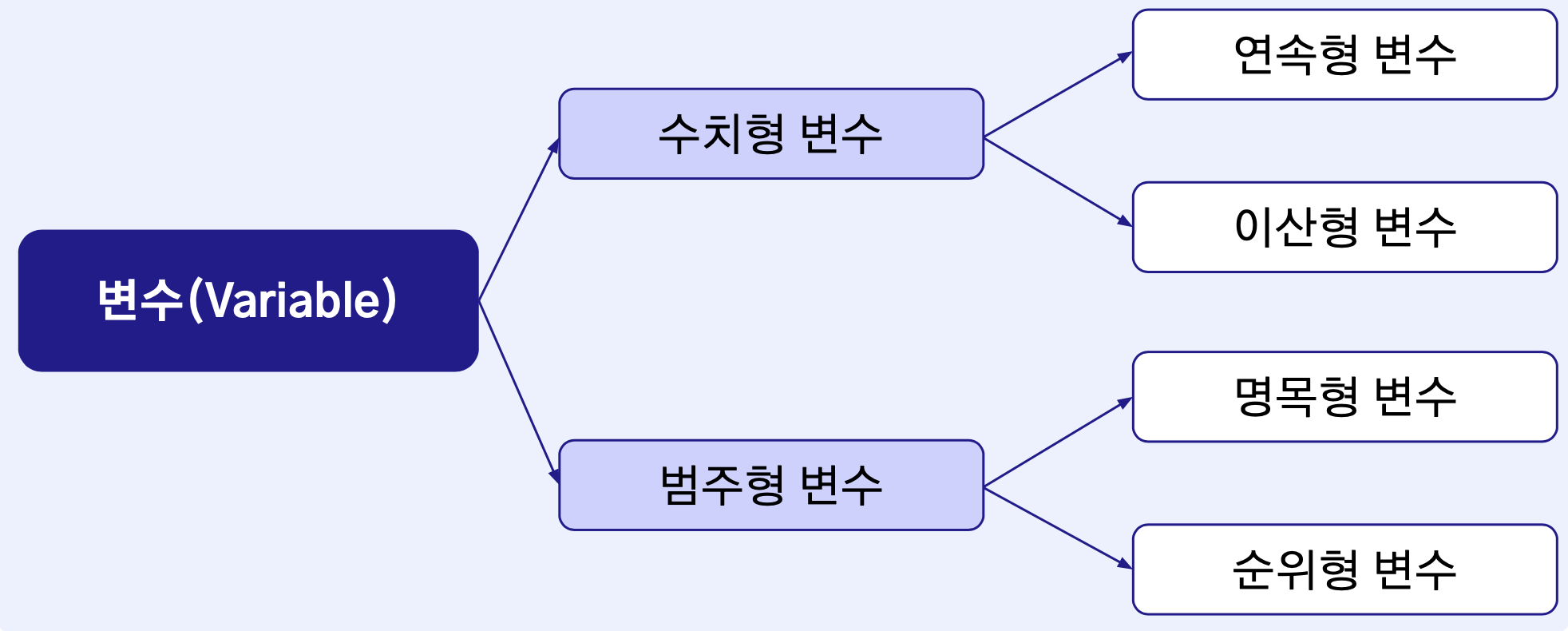
- 변수는 크게 수치로 표현할 수 있으면서 수학적 연산이 가능한 경우 수치형 변수(Numerical Variable), 그렇지 않은 경우 범주형 변수(Categorical Variable)로 구분한다.
- 수치형 변수는 다시 실수 범위 내에서 소수점을 사용하는 연속형 변수와 소수점을 사용하지 않고 정수(이선적)로만 표현하는 이산형 변수로 구분한다.
- 범주형 변수 역시 범주에 순위가 존재하는가에 따라 명목형(순위가 없음) 변수와 순위형 변수로 구분한다.
3.결측치(Missing Value)
3-1.정의
결측치는 값이 누락된 데이터를 말한다. 관측시 장비 이상으로 관측된 값이 없거나 기록하는 과정에서 문제가 생기는 등 발생하는 원인은 매우 다양하다. 결측치는 보통 N/A(Not Available), NaN(Not a Number), NULL, Empty, ? 등 다양한 방식으로 표기되며 도메인에 따라 0도 결측치로 취급할 수 있다.
3-2.결측치 발생 매커니즘
이번엔 결측치가 어떻게 발생했는지 정리해보자. 이 부분은 꽤나 의미 있는 부분이 될 수 있는데, 보통은 결측치가 단순히 값이 누락되었으니 어떻게 처리할지를 고민할 뿐 “왜 생겨났는지”에 대해서는 생각하지 않는다. 이러한 발생 원인에 대해 알 수 있으면 결측치가 가진 의미 및 패턴을 정의할 수 있게 된다.
완전 무작위 결측(MCAR : Missing Completely At Random)
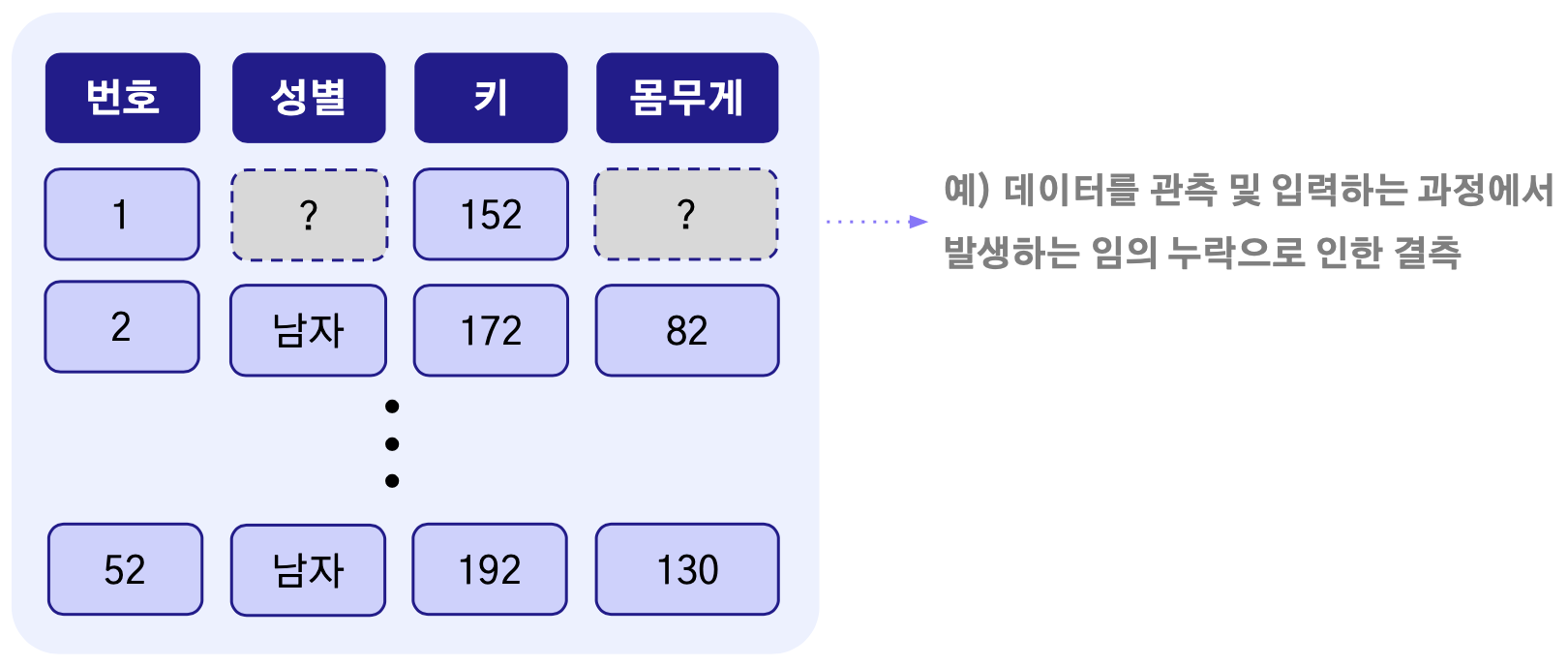
완전 무작위 결측은 결측치가 다른 변수와 상관 없이 무작위로 발생하는 경우로 쉽게 정리하면 결측치를 포함하는 해당 변수 내부적으로도 발생 원인이 없고 다른 변수들과의 연관해서 보더라도 발생한 의미가 없는 결측치를 말한다. 관측 센서가 고장이 났거나 전산적으로 오류가 발생하는 등 다양한 원인으로 발생할 수 있다.
무작위 결측(MAR : Missing At Random)
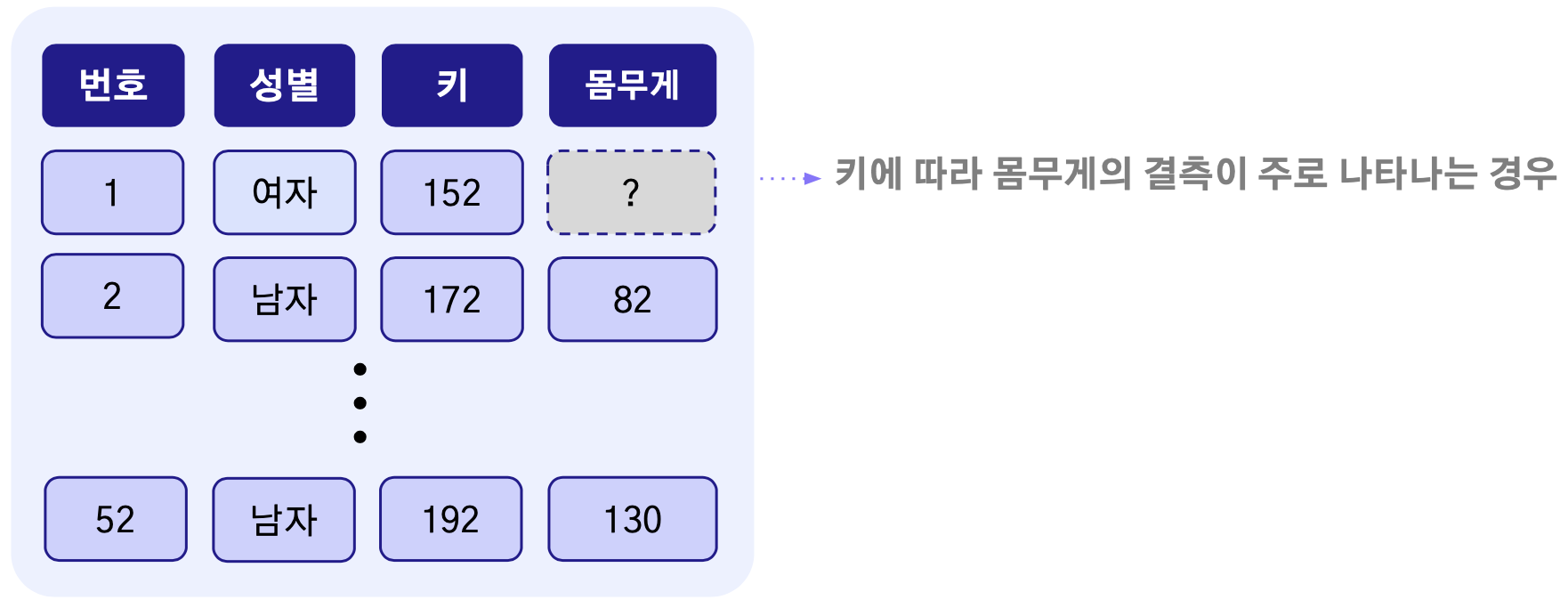
결측치를 보유한 해당 변수 자체적으로는 관계가 없지만 다른 변수와 발생 원인이 연관이 있는 경우다. 다른 변수와 연관이 있기 때문에 예측 모델을 활용해 결측치를 예측값으로 대체할 수 있다. 쉬운 예로 그림에서 보이는 것처럼 성별, 키, 몸무게를 설문조사로 관측한다고 했을 때 “성별이 여자인 사람들이 몸무게를 누락하더라” 혹은 “키가 너무 작거나 큰 사람들이 몸무게를 누락하더라”와 같이 특정 변수에서 결측치가 발생한 원인이 다른 변수와 관련이 있는 경우 무작위 결측에 해당한다.
비무작위 결측(MNAR : Missing Not At Random)
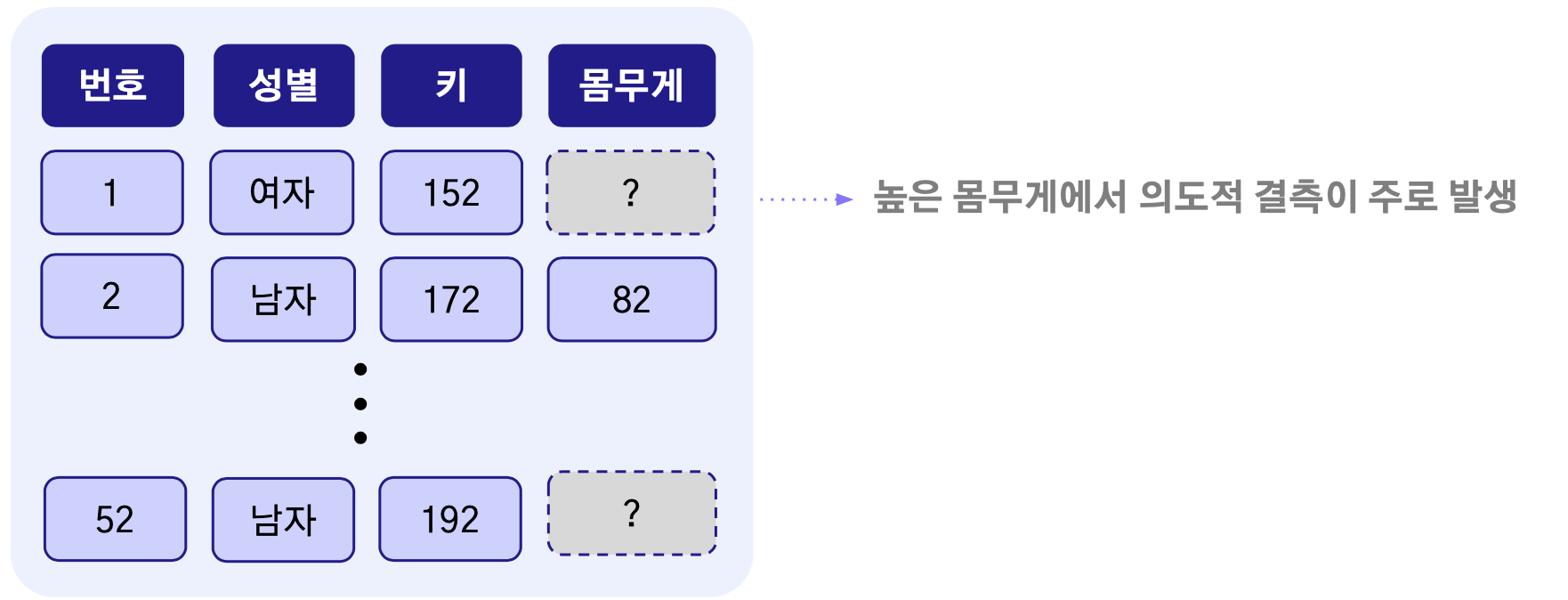
비무작위 결측은 결측치를 보유한 해당 변수 내부적으로 원인이 있고 다른 변수와는 관련이 없다. 쉬운 예로 “몸무게가 너무 작거나 큰 사람들은 몸무게가 컴플렉스여서 누락하더라”와 같이 결측치가 발생한 원인이 해당 변수 스스로에게 있는 것이다.
3-3.결측치 패턴
결측치 패턴에서는 결측치가 데이터셋 내에서 어떻게 구성되어 있는지를 말한다.
1.일변량 결측 패턴(Univariate Pattern)
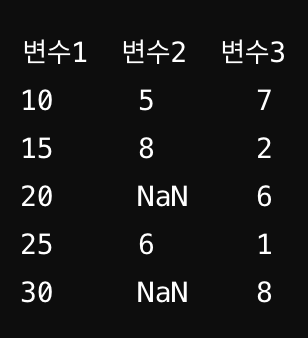
하나의 변수에서만 결측치가 발생한 것으로 다른 변수와는 연관이 없는 형태다. 앞서 비무작위 결측에서 예로든 몸무게가 컴플렉스인 사람이 몸무게 값을 누락하는 것과 같다.
2.단조 결측 패턴(Monotone Pattern)
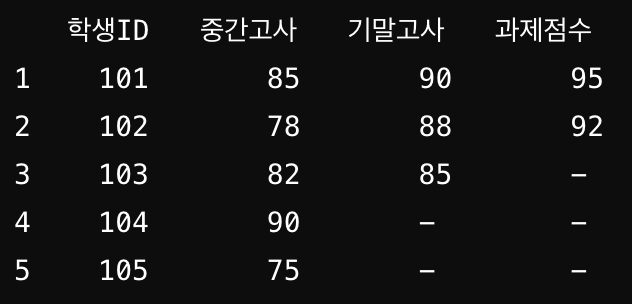
결측치가 일정하고 단조적인 패턴을 보이며 발생한다. 그림에서 보이는 데이터를 해석해보면 “기말고사를 응시하지 않은 학생들은 과제도 제출하지 않더라”와 같은 패턴을 찾을 수 있다. 또 다른 예로 “체력시험에서 달리기 시험에 탈락한 응시생들은 나머지 시험에도 응시하지 않더라” 와 같은 단순한 패턴을 보인다.
3.일반 결측 패턴(General & Non-Monotone Pattern)

단조적이지 않은 형태의 결측치로 다른 변수와의 관계에 따라 결측치가 발생하는 패턴이 비선형적이다. 즉, 결측치가 특정 순서나 규칙 없이 무작위로 발생하며 단조 결측 패턴과 달리 데이터셋 내의 결측치가 여러 변수에서 불규칙하게 나타난다.
4.규칙 결측 패턴(Planned Pattern)
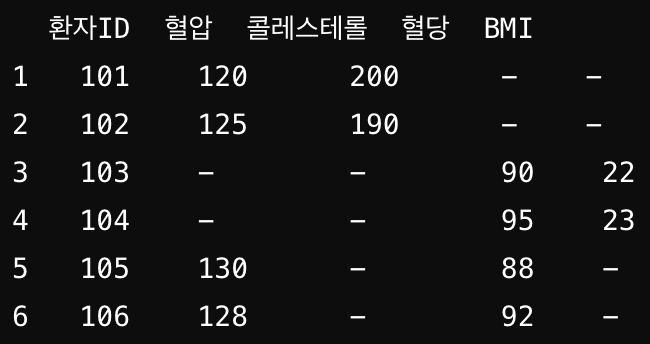
결측치가 발생하는 원인이 일정한 패턴 및 규칙에 따라 발생하며 연구 설계 또는 데이터 수집 과정에서 의도적으로 결측치를 발생시키는 경우를 말한다. 의료 연구에서 새로운 치료법의 효과를 평가하기 위해 여러 가지 건강 지표를 측정하는데 연구자는 시간과 비용을 절감하기 위해 모든 환자에게 모든 건강 지표를 측정하지 않고, 각 환자에게 일부 지표만 측정하도록 설계하여 결측치를 계획적으로 생성하는 경우를 예로 볼 수 있다.
3-4.결측치 처리
지금까지 결측치의 정의, 발생 매커니즘 그리고 패턴에 대해 알아봤다. 이제는 결측치를 어떤 식으로 처리해야할지 정리해보자.
1.목록 삭제(Listwise Deletion), 열 삭제(Dropping Columns)
- 목록 삭제는 변수에 결측치가 존재하는 행(row) 즉, 데이터 샘플을 제거하는 방식으로 모든 변수가 결측치 없이 채워진 행만 분석과 모델리에 활용하는 방식.
- 열 삭제는 결측치가 존재하는 열(column)을 제거하는 방식.
이렇게 결측치가 존재하는 부분을 삭제 하는 것은 결측치를 처리하는 가장 간단하고 빠른 방식이다. 결측치를 삭제하면서 데이터 분포가 왜곡 되는 것과 모델의 성능 향상을 기대하는데 이 방식은 아주 주의해야한다.
- 앞서 봤듯 결측치가 발생하는데는 데이터가 가진 특성하는 것과 마찬가지로 “유효한 특성”이 존재할 수 있다.
- 데이터를 삭제하기 때문에 원래 데이터셋이 가진 분포가 바뀌게 되며 이로 인해 편향적으로 바뀔 수 있다.
- 분석 및 모델 학습에 반영될 데이터의 수가 줄어들기 때문에 손해가 필연적으로 발생한다.
2.대체(Imputation)
대체는 결측치를 제외한 나머지 값들을 이용한 통계값(평균, 최빈값, 중앙값)으로 결측치를 대체하는 것으로 일반적으로 가장 많이 사용하는 방식이다. 해당 변수가 가진 통계적 특성을 반영하기 때문에 안정적이며 삭제되는 데이터가 없기 때문에 전체 데이터를 그대로 사용할 수 있다.
- 다만 결측치가 많은 경우 통계값으로 대체되는 데이터의 수가 많아지므로 해당 변수의 분산이 감소한다. 분산이 낮아진다는 것은 변화량이 적다는 뜻인데 이렇게 되면 다른 변수가 증가하거나 감소하더라도 해당 변수의 값은 그대로라는 말이기 때문에 상관관계가 낮아지는 문제가 발생한다.
- 또한 평균은 이어서 설명할 이상치에 굉장히 민감하기 때문에 잘못된 통계량으로 값을 대체하게 되는 위험도 존재한다.
3.모델을 이용한 대체
이 방법은 말 그대로 결측치를 보유한 해당 변수를 예측하는 모델을 만들어 결측치를 예측값으로 채우는 방식이다. 변수 간 연관성을 활용하여 예측 모델을 학습시키기 때문에 준비 과정에서 데이터에 대한 추가적인 분석 및 인사이트가 발생하는 장점이 있다. 뿐만 아니라 삭제나 통계치로 대체하는 방법보다 실제 데이터와 유사할 가능성이 높다. 물론 단점은 그만큼 정확한 예측을 하는 모델을 만들어야한다는 점으로 자칫 잘못하다간 배보다 배꼽이 더 커질 수도 있다.
4. 이상치(Outlier)
4-1.정의와 발생 원인
이상치는 변수의 분포상 비정상적으로 극단적인 값을 말한다. 쉽게 말해 다른 데이터 샘플들의 값보다 현격히 차이나는 값으로 그래프 상에서 혼자 동떨어진 모습을 보인다. 이상치는 일상 속에서 쉽게 접할 수 있는데 2030 평균 연봉을 조사했을 때 상위 0.x%의 사람들이 억대 연봉을 받고 있는 사람들이 이상치에 속한다. 이로 인해 2030 평균 연봉이 높아지는 왜곡이 발생한다.
이상치가 발생하는 원인은 결측치와 마찬가지로 굉장히 다양하다. 앞서 본 예처럼 억대연봉을 받는 사람이 발생한 원인은 그냥 그 사람의 연봉이 높기 때문이며 이외에도 해킹으로 인해 의도적으로 값을 이상하게 바꾸었다거나 데이터 수집 기기나 알고리즘의 오작동으로 인해 잘못된 값이 기입되었을 수도 있다. 뿐만 아니라 주가 조작처럼 의도적으로 이상치를 발생시킬 수도 있다.
4-2.이상치를 탐지하고 제거해야하는 이유
일단 이상치가 존재하는지 탐색하는 과정에서 분포 확인 및 시각화를 자연스럽게 수행하기 때문에 데이터의 패턴 확인 및 인사이트 도출이 자연스럽게 따라온다. 또한 이상치를 찾고 난 후 적절한 방법을 적용해 제거를 하고 나면 왜곡된 데이터 분포를 정상적으로 만들 수 있고 이에 따라 모델 학습의 안정성과 일반화 성능을 높이는데 기여한다.
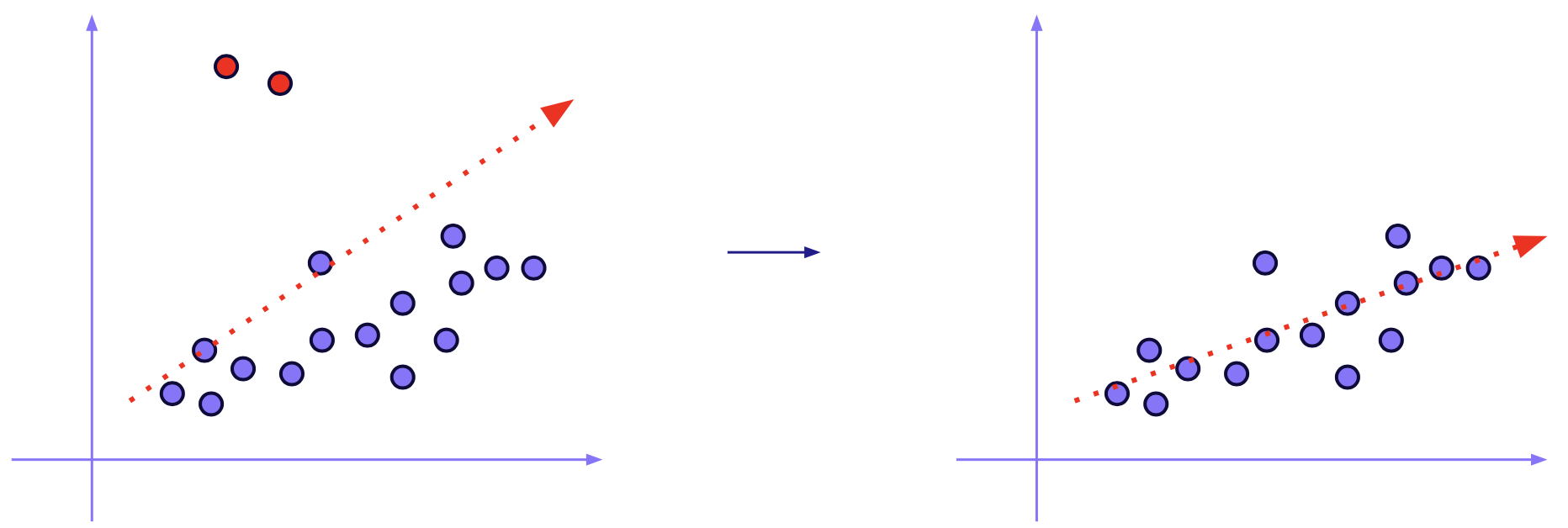
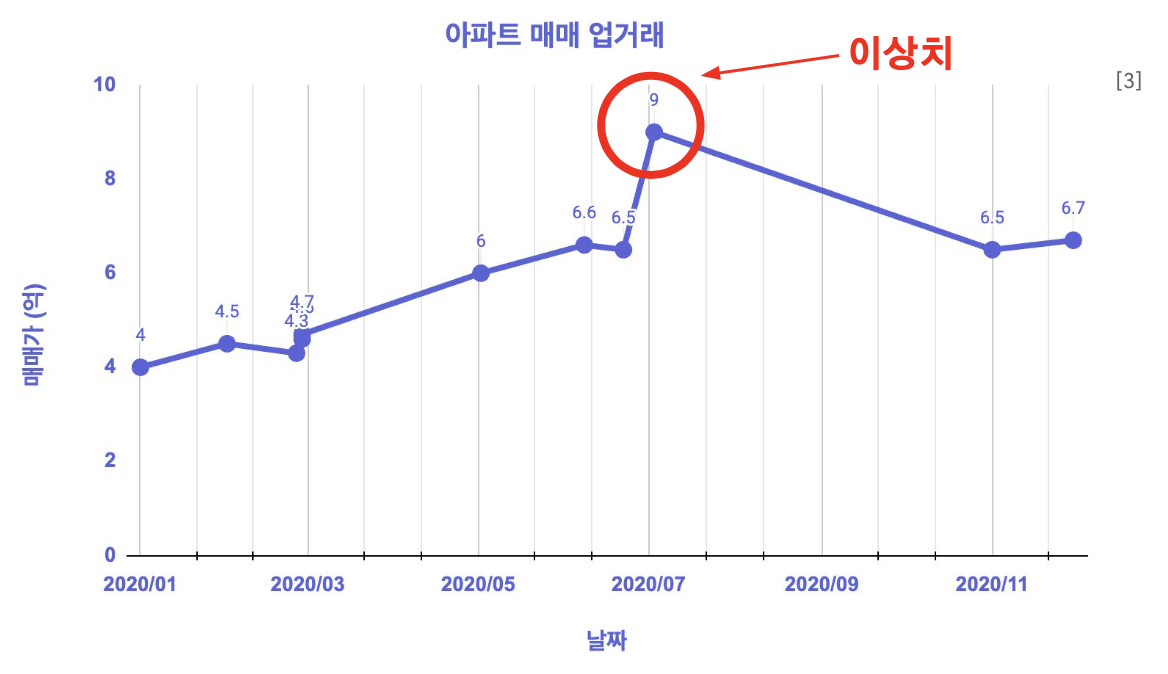
가장 쉬운 예로 그림처럼 선형 회귀 모델을 학습 시키는 상황을 가정해보자. 선형 회귀 모델은 데이터 포인트들을 가장 잘 대표하는 직선을 찾는 것으로 이 직선은 각각의 데이터 샘플들과의 오차 합이 최소가 되는 직선이다. 하지만 왼쪽과 같이 이상치가 존재하는 경우 이상치까지 감안해서 최적의 직선을 찾으려다 보니 오른쪽 그림처럼 globally optimal한 직선을 찾을 수 없게 된다.
4-3. 이상치의 종류
1.점 이상치(Point Outlier)
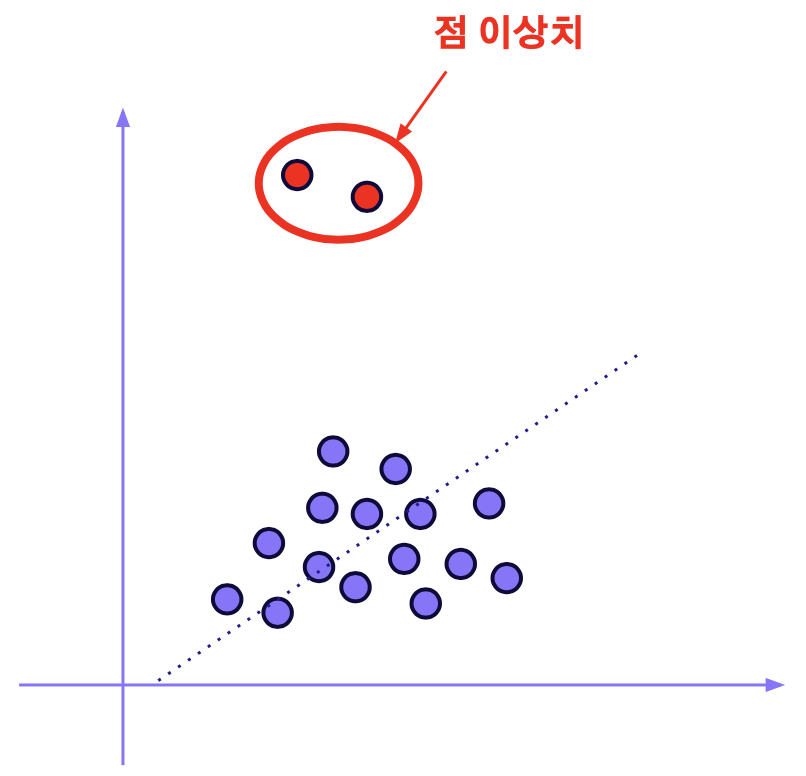
대부분의 관측치들과 거리가 멀리 떨어진 형태로 분포를 확인했을 때 쉽게 알아볼 수 있다.
2.상황적 이상치(Contextual Outlier)
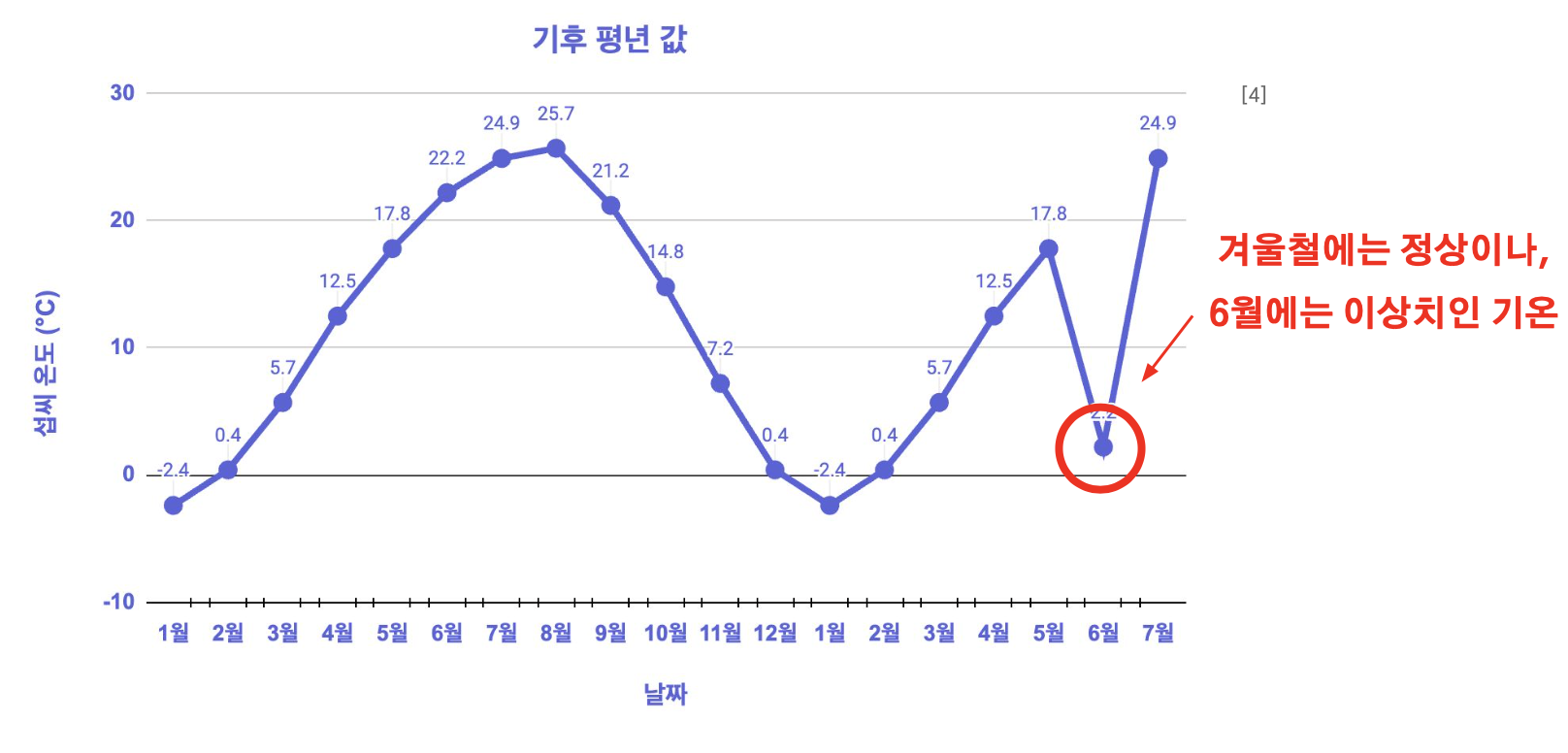
정상적인 데이터 패턴이라도 상황에 따라 이상치로 취급되는 형태다. 예를 들어 “아이스크림이 1000만개가 팔렸다.”라는 것은 이상치가 아니라 정상적인 패턴으로 인지할 수 있지만 “겨울철에 아이스크림이 1000만개가 팔렸다.”라는 상황이 추가되면 이상치로 취급할 수 있다.
3.집단적 이상치(Collective Outiler)
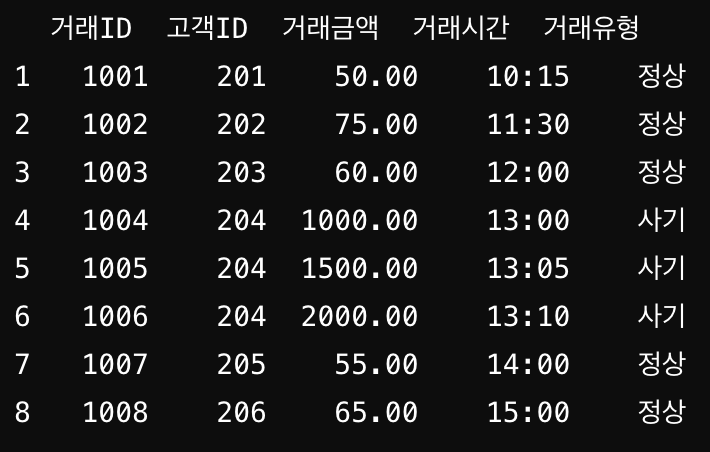
산점도를 그렸을 때 데이터 샘플들이 평범하게 군집을 형성하는 것처럼 보이지만(일반적인 데이터 샘플들과 거의 유사) 한 집단 전체가 다른 데이터와 비교했을 때 극단적으로 다른 값을 가지는 경우를 말한다. 주어진 예를 보면 정상적인 데이터는 100만원 미만의 거래가 긴 시간 간격동안 발생하지만 특정 데이터들은 짧은 간격에 1000만원 이상의 큰 금액들이 거래된 것을 확인할 수 있다.
4-4.이상치 탐지
Z-Score
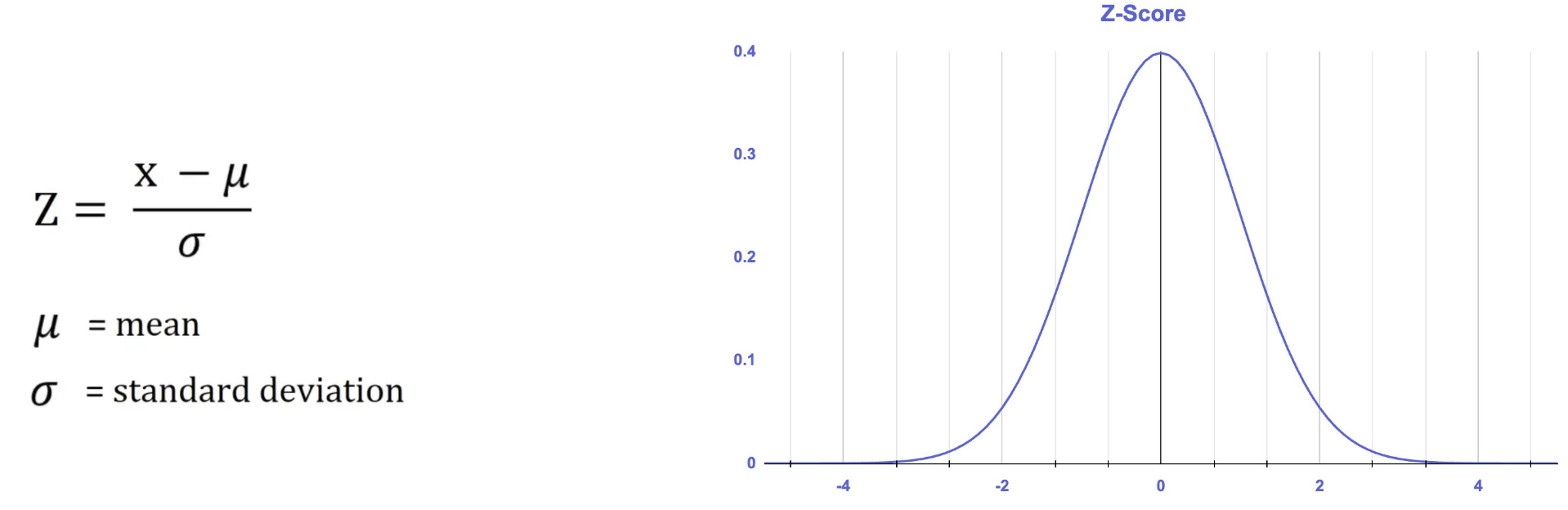
변수의 수치 범위(값의 크기 범위)를 평균이 0, 표준편차가 1이 되도록 변환하는 것으로 쉽게 말해 각각의 데이터 샘플들을 평균과의 거리(표준편차)로 변환한 것이다. 가장 일반적으로 많이 사용하는 탐지 방법으로 Z값이 2.5~3.0 정도로 나오면 이상치라고 판별한다. 변수가 가진 데이터가 정규분포를 따른다고 가정을 하는 방식이기 때문에 정규분포 형태가 아닐 때는 그다지 효과적이지 않을 수 있으며 평균과 표준편차는 이상치에 매우 민감하기 때문에 평균이 신뢰할 수 있는 값인지 반드시 확인하고 적용해야한다.
IQR
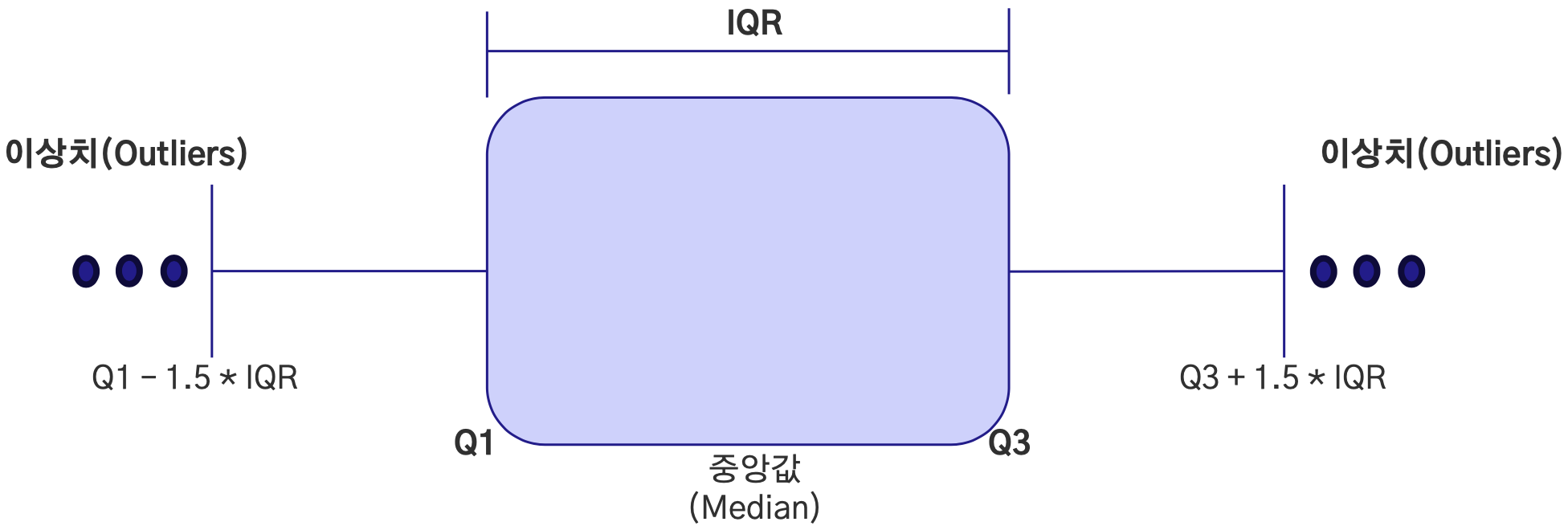
사분위수에서 “3사분위수(Q3) - 1사분위수(Q1)”에 해당하는 구간을 말한다. 이 구간을 기준으로 $Q1 - 1.5 * IQR$ 및 $Q3 + 1.5 * IQR$을 최극단의 이상치로 판단하여 처리하는데 이는 중앙값과 분포를 이용해 이상치를 식별하는 방식이기 때문에 이상치에 강건하다. 무엇보다 수염 그래프를 통해 직관적으로 시각화 및 해석이 가능하기 때문에 효과적인 방법인데, 단점이라면 왜도가 심해 정규분포를 따르지 않을 때 제대로 작동하지 못할 가능성이 존재한다.
4-5.이상치 처리
1.삭제와 대체
이상치도 결측치와 마찬가지로 삭제 또는 대체하는 것이 가능하다.
- 이상치에 해당하는 데이터 샘플을 제거하는 것은 가장 단순하다.
- 하지만 이상치가 “의미있는 특성”을 내재하고 있는 경우도 있기 때문에 꼼꼼한 EDA를 기반으로 한 정확한 분석이나 도메인 지식을 기반으로 제거하는 것이 올바른 결정인지 판단해야한다.
- 대체 할 때는 통계치를 활용할 수 있으며 분석을 통해 설정한 상한 및 하한을 넘어갈 때 대체하는 편이 좋다. 뿐만 아니라 예측모델을 생성하여 적절한 값으로 대체하는 방법도 있다.
2.변환(Transformation)
이상치는 삭제, 대체 이외에도 이상치를 적절한 값으로 바꾸는 변환 방식도 존재한다. 대표적으로는 로그(Log), 제곱근, 거듭제곱, Box-Cox 변환 방식들이 있는데, 이 방식들은 변수를 다룰 때에도 해당되는 내용이기도 하고 글이 너무 길어진 상태이기 때문에 다음 글에서 정리하고자 한다.
댓글남기기