Deep Learning Basic

2023년부터 지금까지 딥러닝의 기본을 반복적으로 학습하면서 여러 차례 정리를 해왔지만, 기록하던 플랫폼을 이래저래 옮기다보니 흩어진 부분들도 많고 이전에 작성했던 것들은 내용이 모자란 것들도 있는 것 같다.

이번에야말로 마지막 끝판왕 정리를 하고자 하는데, 최대한 잡설은 빼고, 개념은 Deep하게 정리할 것이다.

1.규칙기반부터 DL까지

과거의 인공지능은 사람이 모든 것을 다 설계했다. 사람이 데이터로부터 여러 개의 특징들을 추출하고 그값들을 정리해 여러 개의 규칙으로 정의한 하나의 소프트웨어인 것이다.
이렇게 소프트웨어가 완성되면 입력된 값으로부터 특징값들을 추출하고 여러 규칙들에 대입하면서 결과값을 산출해낸다. 이러한 방식의 AI를 규칙 기반 프로그래밍이라고 하며 사람이 AtoZ로 모든 것을 설계하고 만들어야했다. 따라서 데이터가 가진 모든 특징을 제대로 추출할 수도 없으며 필수적인 규칙을 놓쳐 잘못된 예측을 하는 경우가 다반사다.

규칙기반의 다음 버전이 우리가 익히 알고 있는 Machine Learning 방식이다. 이 단계에서도 여전히 어떤 특징을 사용할지 그리고 그 값은 어떻게 계산할지는 모두 사람이 설계하지만 입력된 tabular data로부터 예측값을 구해내는 규칙은 모델이 스스로 찾아낸다. 이러한 방식은 효과가 꽤나 좋았지만 사람이 설계, 정의하는 hand craft feature는 너무나도 비쌌고 성능은 그에 비례하지 못하는 상황이었다.

끝판왕인 Deep Learning은 사람이 특징을 설계할 필요없이 데이터만 입력하면 Neural Network가 알아서 필요한 특징들을 추출하고 이들로부터 정밀한 예측을 하기 위한 규칙을 스스로 찾아낸다.
물론 AtoZ가 모두 자동인 것은 아니다. Neural Network를 어떻게 설계하는가에 따라 성능 차이가 매우 클 수 있고, 데이터를 적절하게 전처리해야하는 것은 여전히 남아 있다. 그럼에도 신경망 기반의 딥러닝은 분명 혁신 그자체였고 AlphaGo부터 ChatGPT, 그리고 언젠가 등장할 AGI까지 AI는 곧 Deep Learning이라고 말해도 과언이 아니다.

이렇게까지 혁신적인 이유는 역시 학습에 반영될 특징값을 사람이 설계하지 않는다는 점과 신경망이 갖는 수많은 파라미터 덕분일 것이다.
앞서 말한대로 사람이 수작업으로 만드는 특징(feature)는 한계가 명확하다. 어떤 특징을 사용할지 파악하는데도 많은 시간이 소모되고 특징값을 추출하는 연산을 정의하는데도 많은 시간이 소모되니 발전이 늦다. 하지만 신경망 기반의 딥러닝은 수많은 파라미터(weight)를 사용해 특징 추출과 예측값 산출을 수없이 반복하니 인간보다 좋을 수 밖에 없다고 생각한다.

2.신경망은 어떻게 학습하는가?

신경망이 학습하는 방식은 크게 네가지 단계로 정리할 수 있다.

  1. Forward Propagation
  2. Loss Function
  3. Back Propagation
  4. Optimization

각각이 무엇을 의미하는지 하나씩 차근차근 알아보자.

설명의 편의를 위해 Supervised Learning으로 학습한다고 가정하자. 쉽게 말해 데이터마다 정답이 있으며 이것을 활용하는 학습 방법이다.

2-1.Forward Propagation

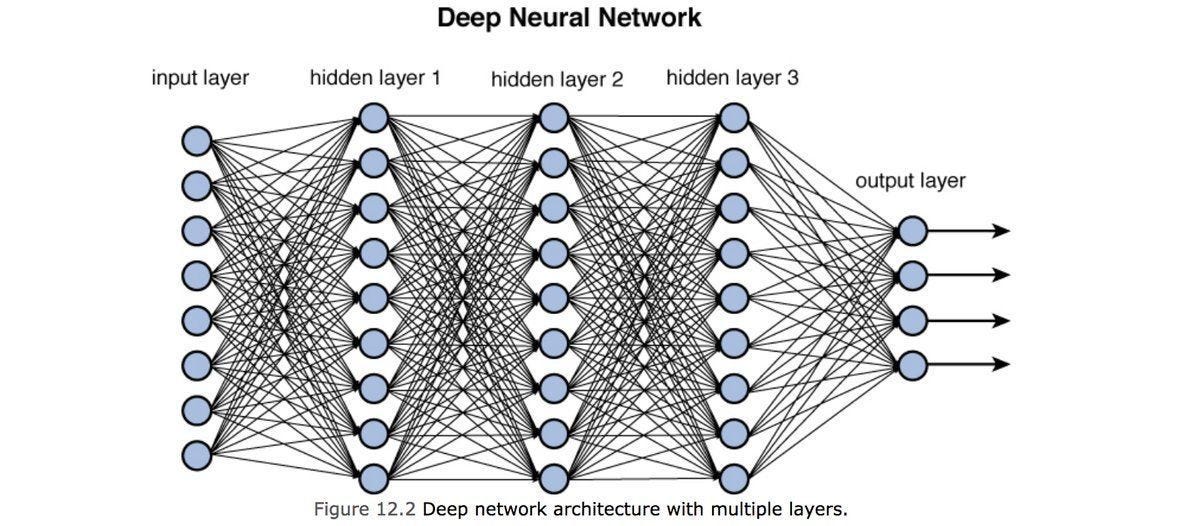
우리말로 “순전파”라고 하는 이 단계는 입력값이 신경망의 구조를 따라 일련의 연산을 거쳐 예측값을 출력하는 단계다.
흔히 MLP, CNN, RNN, Transformer와 같은 것은 모두 신경망을 설계하는데 적용된 연산이 다른 것으로 MLP는 fully connected layer, CNN은 convolution, Transformer는 Attention을 이용해서 입력된 값을 예측값으로 변환, 매핑하게 된다.

2-2.Loss Function

forward 단계에서 출력한 예측값은 정답값과 함께 손실함수에 입력되어 오차를 출력하게 되는데 이는 곧 모델의 예측이 얼마나 나쁜지 정량적으로 평가하는 것과 같다.
신경망은 수많은 파라미터를 가지고 있다고 했는데, 반복하는 매 단계별로 파라미터의 값을 다르게 설정하게 된다. 따라서 현재 단계의 파라미터 값을 기준으로 만든 예측이 정답과 얼마나 오차가 큰지 계산하고 이것을 피드백 삼아 파라미터를 어떻게 업데이트할지 결정한다. 이렇게 업데이트된 파라미터로 다시 한 번 예측을 구하고 오차를 계산하는 방식을 반복한다.

참고로 손실함수도 “함수”이기 때문에 어떤 함수를 적용하는가에 따라 학습의 방향이 달라지게 된다.

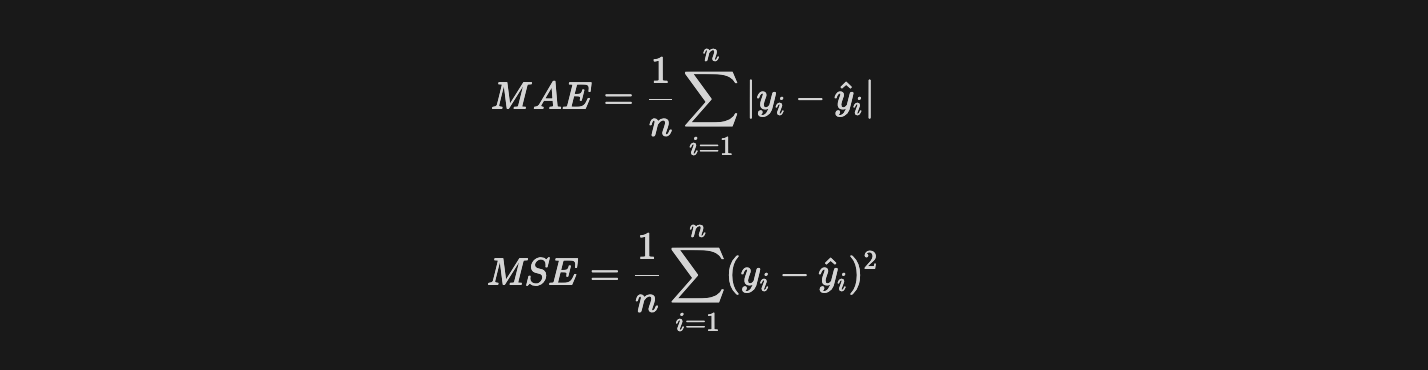
주어진 두 개의 손실함수 MAE(Mean Absolute Error)와 MSE(Mean Squared Error)는 오차에 절대값을 적용하는지 혹은 제곱을 적용하는지 정도의 차이다. 사소해보이지만 이것만으로도 학습에 대한 컨셉이 달라진다.

  • MAE는 절대값이므로 모든 오차를 동등하게 다룬다. 따라서 이상치가 없는 데이터셋을 사용하여 균일한 오차를 분포를 갖는 예측 결과를 얻는 경우에 적합하다.
  • 반면 MSE는 제곱에 의해 오차가 크면 클수록 제곱으로 증폭된다. 따라서 이상치로 인한 큰 오차가 발생하는것에 크게 반응한다.(이상치에 매우 민감함.)

2-3.Back Propagation

back propagation은 역전파라고 불리는데, 손실함수로 구한 피드백을 신경망의 출력층에서 시작해 입력층의 방향으로 전달하는 단계다. 신경망은 기본적으로 여러 개의 층으로 구성되고 각 층은 고유한 파라미터를 보유하고 있기 때문에 이들의 값을 업데이트하기 위해서는 역전파가 효과적이다.

역전파가 왜 효율적인 방식인지는 이어지는 최적화 알고리즘에서 다루고, 역전파가 어떻게 계산되는지부터 알아보자.

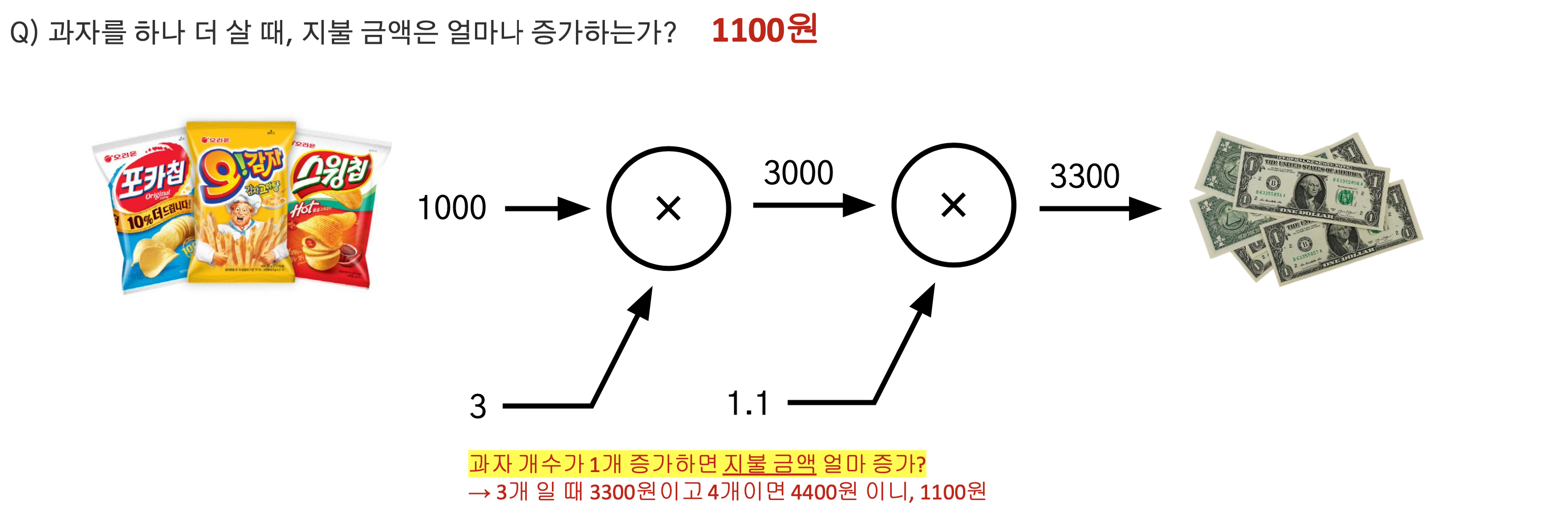
딥러닝을 공부해본 사람이라면 다음과 같은 계산그래프(Computational Graph)를 본 적이 있을텐데 여기서 말하고자 하는 것은 “최종 출력값에 영향을 주던 변수들 중 하나의 값이 변했을 때 최종 출력값은 어떻게 변하는가”를 구하는 것이다.

  • 이는 수학적으로 미분의 정의인 “x값이 변화했을 때 함수값 y=f(x)의 값이 얼마나 변하는가”와 동일하다.
  • 따라서 신경망의 학습은 “여러 층이 가진 각각의 파라미터 값이 바뀌었을 때 손실함수의 값이 어떻게 변하는가” 즉, 손실함수에 대한 각각의 파라미터를 편미분을 계산하여 업데이트할 양을 계산하게 된다.

전체 역전파 과정은 다음과 같이 정리할 수 있는데, 기본적으로 신경망을 구성하는 각 층은 입력값을 받아 출력값을 산출함을 기억하자.

1.출력층의 Gradient

  • 식(1) : 손실함수 값에 대한 출력층 파라미터의 편미분이자 Gradient인 $ \frac{\partial L}{\partial A^l} $를 계산한다.
  • 식(2) : $ \frac{\partial L}{\partial A^l} $가 선형변환 층 $ Z^l $로 전달되어 $ \frac{\partial L}{\partial Z^l} $를 계산한다.
  • l번째 층의 활성화 함수에서 전달한 gradient는 l번째 선형변환 층 기준에서 보면 “상류”에서 전달한 것으로 비유할 수 있는데 이에 따라 $ \frac{\partial L}{\partial A^l} $를 Upstream Gradient라고 한다.
  • 또한 선형변환 층의 출력값 $Z^l$에 대해 입력 $A^{l-1}$에 대한 편미분 $ \frac{\partial L}{\partial A^{l-1}} $과 학습 파라미터 $W^{l}, \ b^{l}$에 대한 편미분 $ \frac{\partial L}{\partial W^l} $, $ \frac{\partial L}{\partial b^l} $을 계산할 수 있는데 이들을 Local Gradient라고 한다.

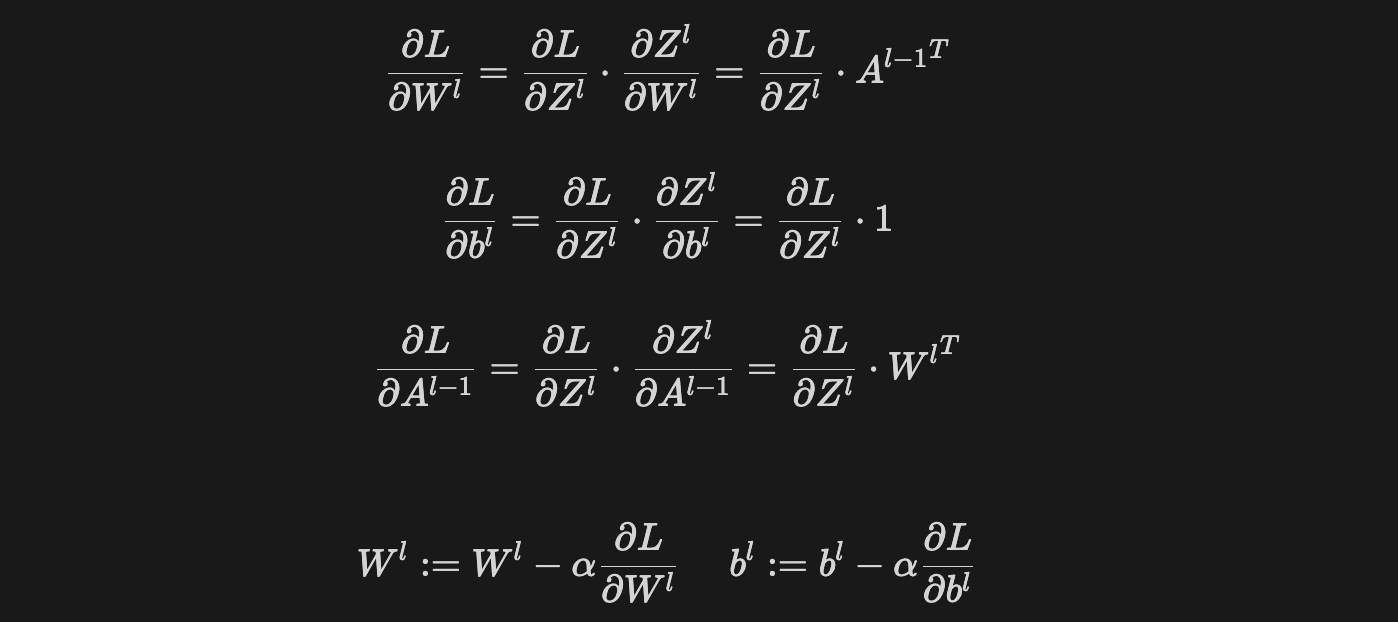
  • 활성화 함수는 학습 파라미터가 없는 비선형 변환이지만 선형 변환 층에는 weight와 bias가 존재한다.
  • $\frac{\partial L}{\partial W}, \ \frac{\partial L}{\partial b} $ 는 해당 파라미터들을 갱신시키며 $\frac{\partial L}{\partial A^{l-1}}$ 은 이전 층(하류)로 전달된다.

2.l-i번째 층의 Gradient

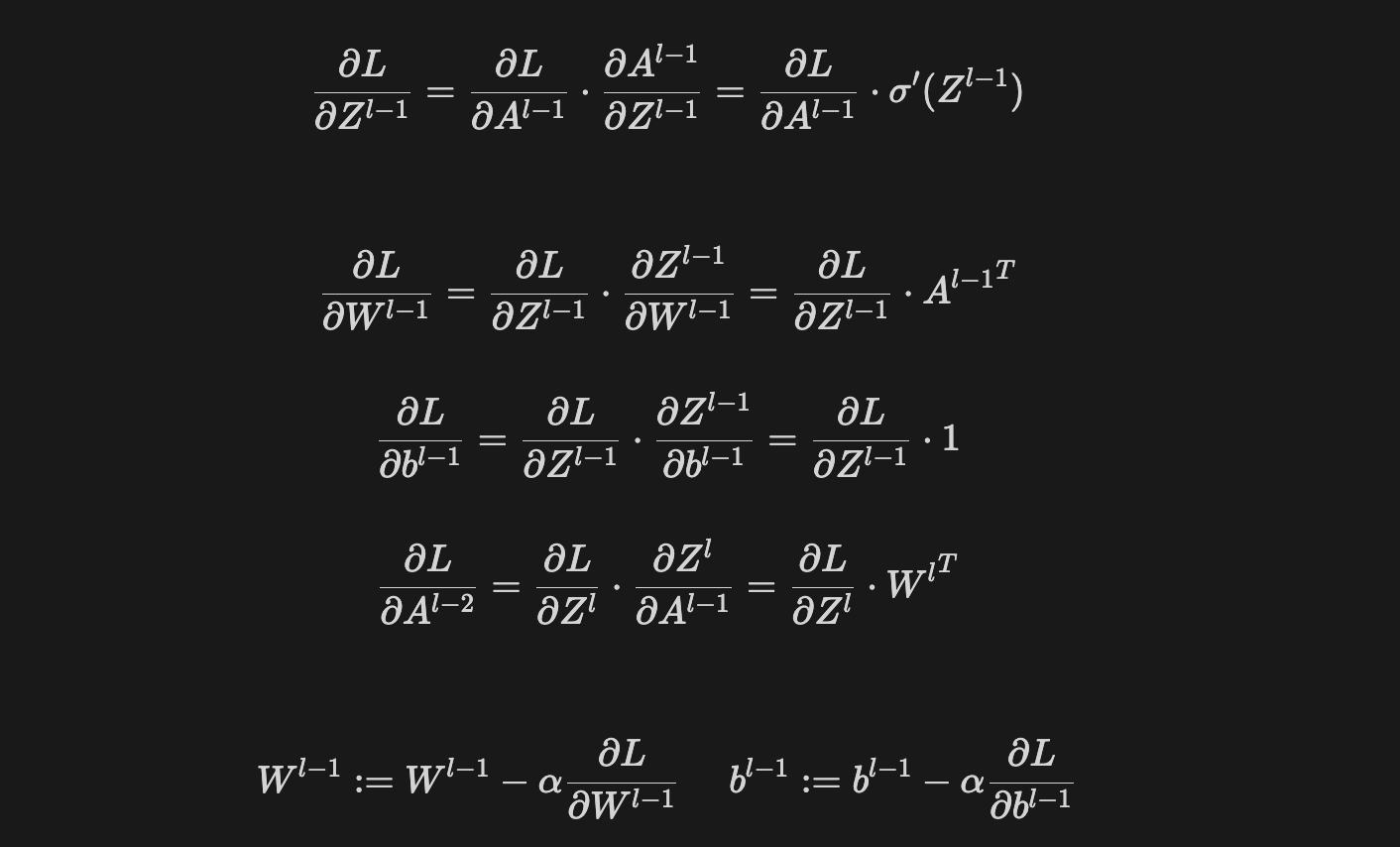출력층($l$번째 층)에서 전달한 Upstream gradient는 l-1번째 층으로 전달되고 l-1번째 층의 local gradient와 chain-rule을 계산하게 된다. 전체 과정은 출력층과 동일하기 때문에 부가적인 설명은 생략한다.

앞서 출력층에서는 강조하지 않았지만 식을 보면 활성화 함수의 미분 $ \sigma^{\prime}(Z^{l-1}) $이 곱해진 것을 확인할 수 있는데 Sigmoid나 Tanh 같은 함수에서 Vanishing Gradient 문제가 발생하는 이유가 바로 이것이다.

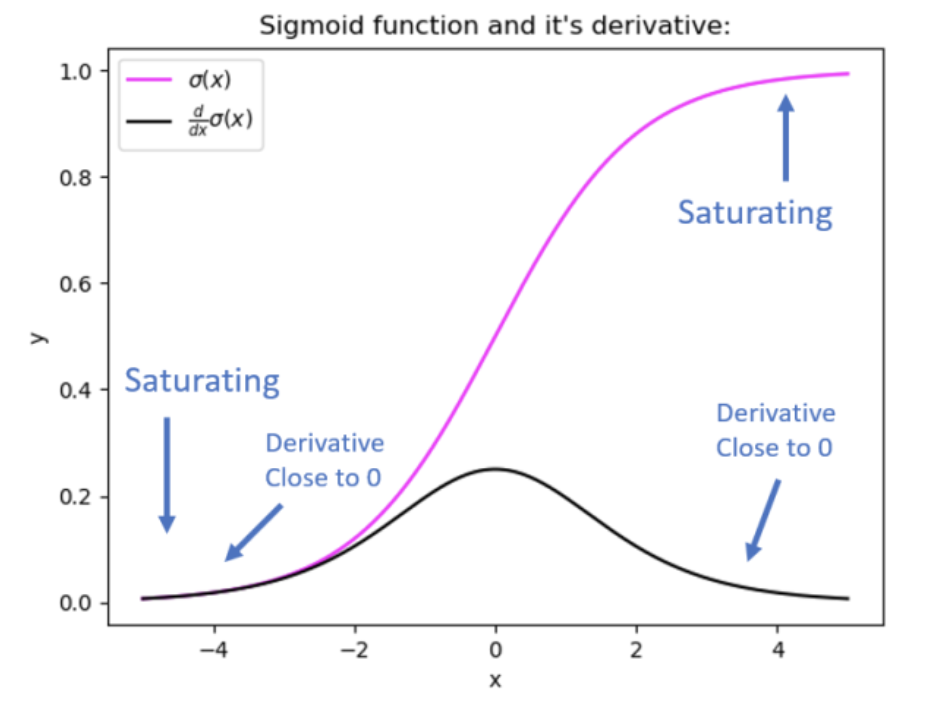
  • 두 가지 활성화 함수는 미분했을 때 기울기가 0이 되는 Saturated Region이 존재.
  • 이에 따라 신경망을 구성하는 층이 깊을수록 역전파 과정에서 지속적으로 0이 곱해져 입력층에 가까운 층들은 파라미터 업데이트가 수행되지 못한다.

2-4. Optimization

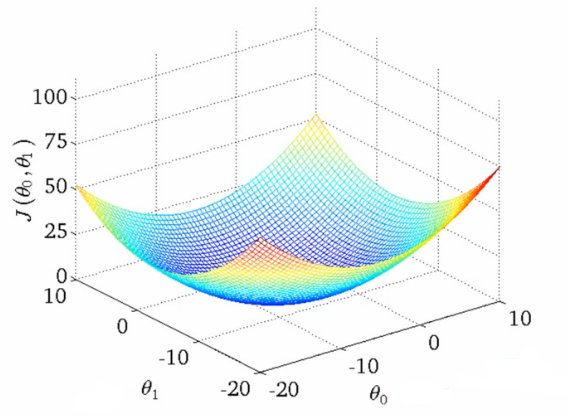
주어진 그림은 입력 $\theta_0$와 $\theta_1$에 따른 함수값들을 특정 범위내에서 구하고 시각화한 것이다. 설명을 위해 해당 함수를 손실함수, $\theta_i$를 학습 파라미터라고 가정하자.

그래프를 보면 손실함수 공간에서 전역적(global)으로 함수값(오차)이 최소가 되는 지역을 한 눈에 알아볼 수 있다. 즉, 전역적으로 최소가 되는 공간을 수학적으로 찾을 수는 있다. 하지만 우리가 딥러닝에서 사용하는 신경망은 함수값을 결정하는 파라미터가 수만개에서 수천억개로 매우 많으며 수많은 학습 데이터(입력값)과의 조합을 모두 따져야하므로 전역적으로 최소가 되는 지역을 찾기엔 시간과 비용이 너무 많이 소모될 것이다.

따라서 손실함수 공간의 값을 모두 계산하지 않고, 신경망의 학습을 시작할 때는 손실함수 공간의 임의 지점에서 시작한다. 쉽게 말해 신경망이 가진 파라미터들을 랜덤으로 초기화 시켜주는 것이다. 여기서 한 가지 문제가 떠오를텐데, 바로 손실값이 최소가 되는 지점을 어떻게 찾는가이다. 분명 궁극적인 목표는 손실값이 최소가 되는 지점을 찾아가는 것인데 임의의 지점에서 시작하면 최소인 지점을 어떻게 찾아갈까??

그 해답은 앞서 봤던 손실함수값에 대한 파라미터의 편미분인 Gradient를 계산하고 Chain-Rule기반 역전파를 수행하는 것이며 이 과정을 학습 과정에서 수차례 반복하면서 파라미터들을 업데이트하면서 오차를 줄여 손실함수 값이 최소가 되는 지점을 찾아가는 것이다.

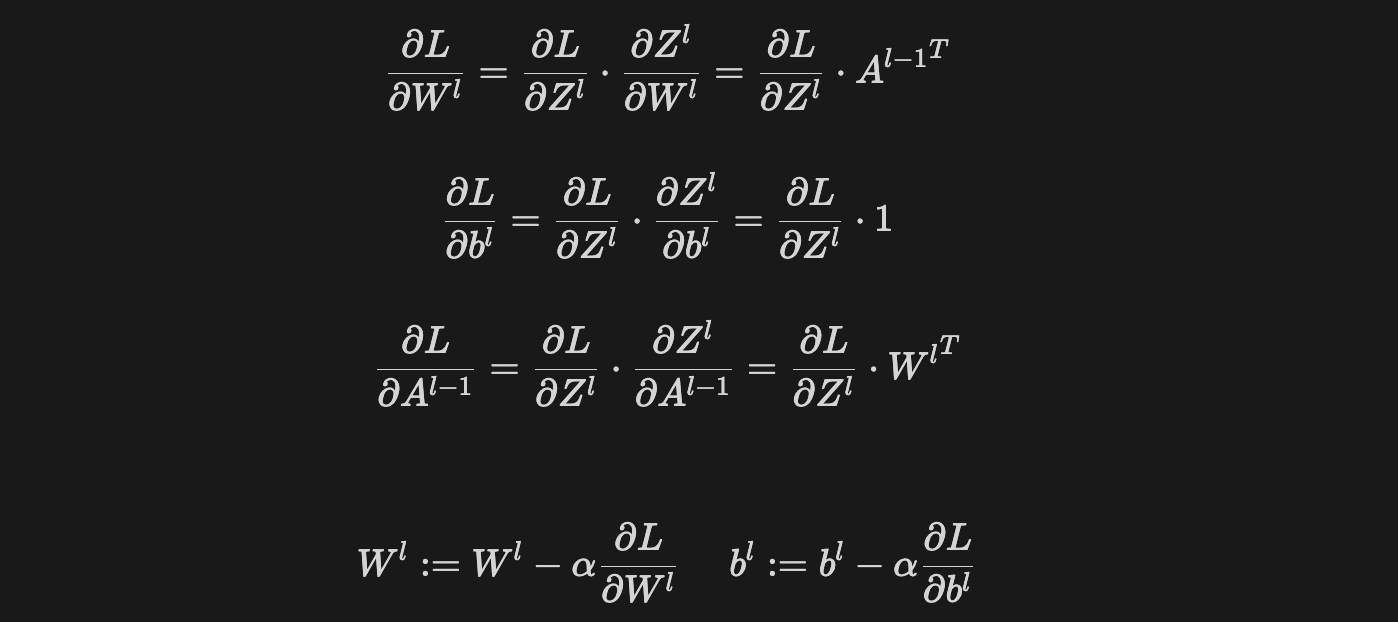
파라미터를 업데이트하는 수식에서 마이너스 기울기를 현재 파라미터 값에 적용하는 것을 볼 수 있는데 이는 음의 기울기 방향으로 이동함으로써 손실함수 값이 감소하는 방향으로 파라미터를 갱신하는 것이다. 이렇게 하면 손실함수 전체 공간에서 전역적인 최소지점을 찾는 것보다 연산 효율성이 높아진다는 장점이 있다. 또한 손실함수 값이 최소가 되는 지점에 가까워질수록 gradient 역시 작아지게 되므로 이러한 학습 방식을 Gradient Descent라고 한다.

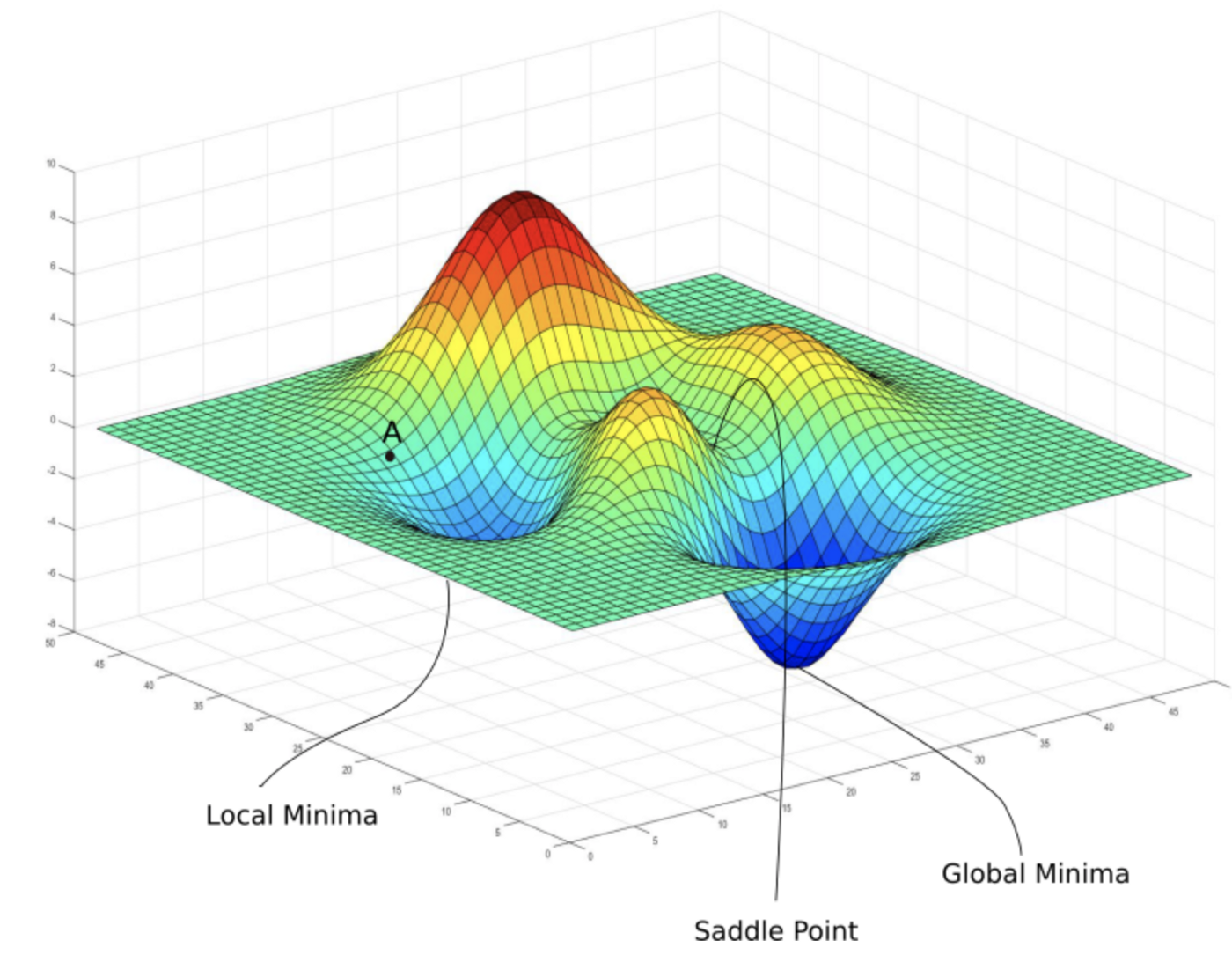
물론 Gradient Descent에는 단점도 존재한다. 손실함수가 앞서 본 그림처럼 아래로 볼록한 함수가 아닐수도 있고, Local Minima나 Saddle Point라고 하는 기울기가 0이 되는 지점이 존재하는 경우 해당 지점을 전역적으로 최소인 지점으로 착각해 학습이 더 이상 진행되지 않는 문제가 발생할 수 있다. 이러한 문제를 해결하기 위해 Gradient Descent을 응용한 최적화 알고리즘들이 개발되기도 하고, 아예 시작점을 전역 최소지점에 가까운 곳으로 설정하기 위한 Weight Initialization 방법들도 개발되고 있다.

3.역전파 실습

지금부터 해볼 실습은 역전파를 수학적으로 이해하는 것이 목적이기 때문에 불필요한 경우 생략해도 좋을 것 같다. 왜냐하면 실제 개발에서는 Tensorflow나 Pytorch 같은 딥러닝 프레임워크를 필수적으로 사용할텐데 거기선 이미 역전파 과정이 모두 구현되어 있기 때문이다. 따라서 역전파의 동작원리를 이해하고 있다면 굳이 읽어보지 않아도 좋다.(나는 그냥 넘어가기 찝찝해서 공부해봤다…)

3-1.네트워크 구성

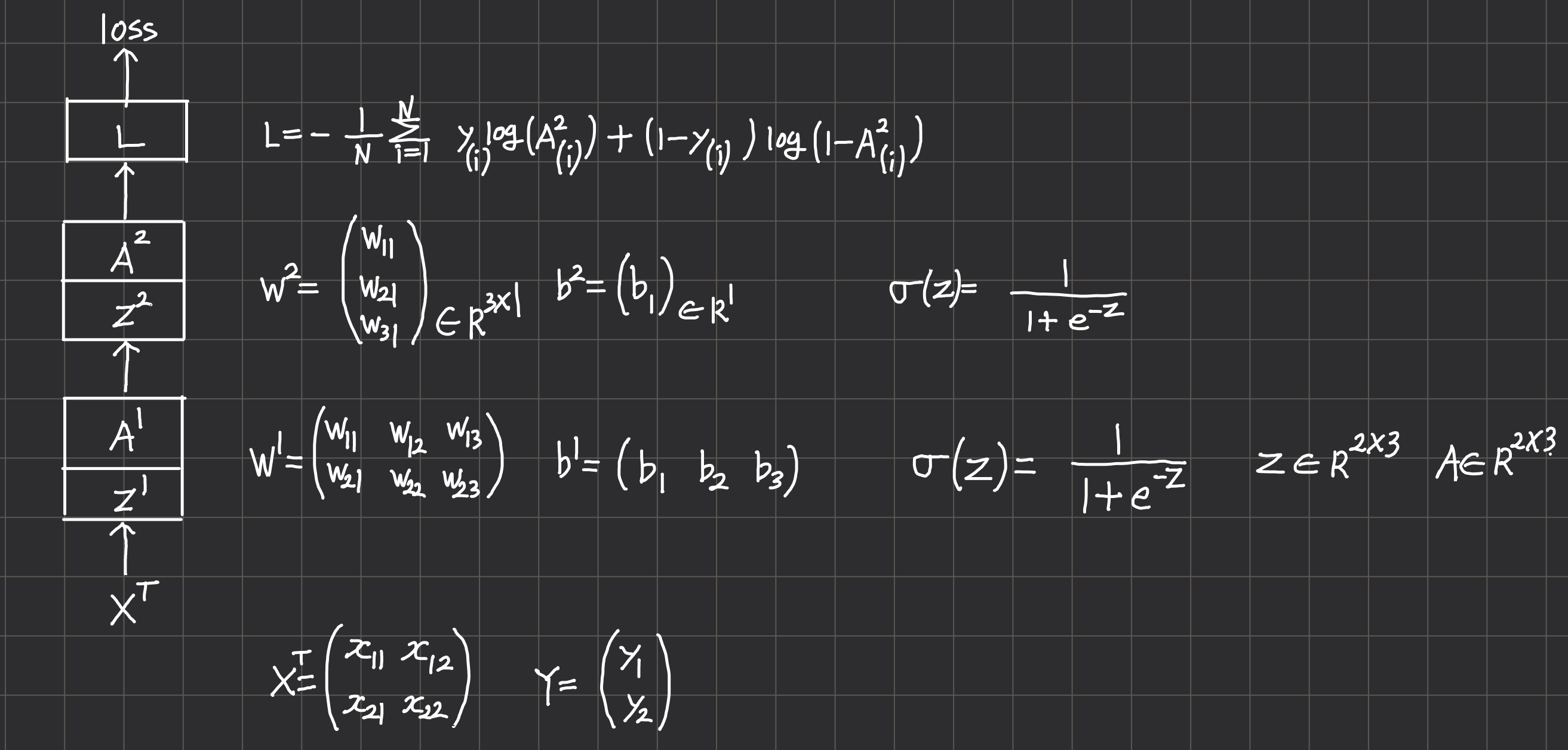
  • 신경망은 은닉층 하나와 출력층 하나로 구성된 2층짜리 네트워크.
  • 각 층의 선형변환은 Linear Layer로 $Z^l = {A^{l-1}}^TW + b $를 계산한다.
  • 활성화 함수는 Sigmoid
  • 손실함수는 Binary Cross Entropy

3-2.Forward Propagation

각각의 데이터 샘플은 두 개의 특징(feature)으로 구성되며 입력은 2개의 데이터 샘플을 포함한 mini-batch이다. 따라서 손실함수는 각 데이터 샘플에 대한 손실을 구하고 평균을 계산하여 반환한다.

3-3.Backpropagation

1.출력층의 gradient

가장 먼저 할 일은 손실함수에 대한 출력층의 미분을 계산하는 것이다.
출력층의 활성화함수가 출력한 값이 모델의 예측인 $ \hat Y $이고 정답 $ Y $ 와 함께 손실함수에 입력되어 손실함수 값을 구했다. 따라서 손실함수에 대한 출력층의 미분은 $ \frac{\partial L}{\partial A^{[2]}} $로 시작한다.

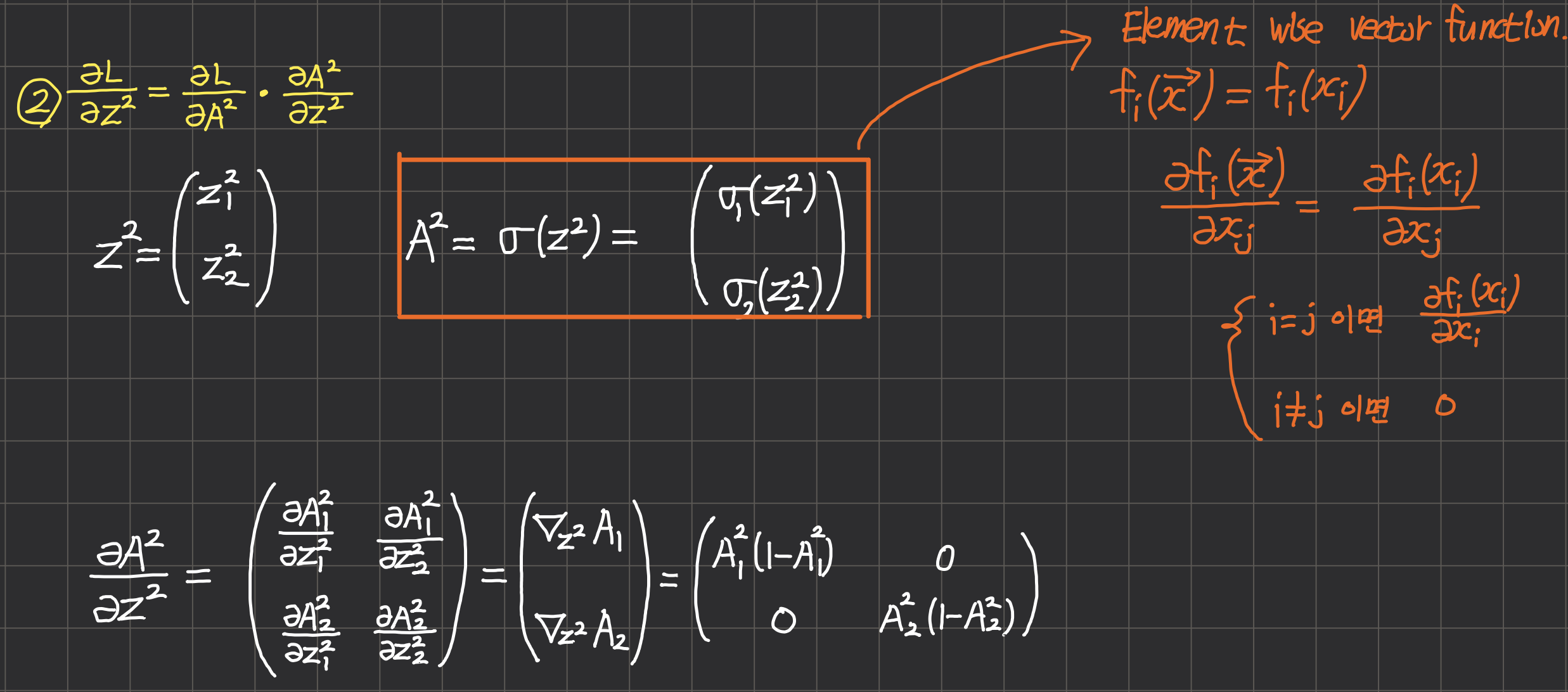
$ \frac{\partial L}{\partial A^{[2]}} $가 선형변환 층으로 전달되며 해당 층에서는 $ \frac{\partial A^{[2]}}{\partial Z^{[2]}} $인 Local Gradient가 있다.

여기서 조금 까다로운 부분은 활성화 함수에 대한 선형변환 층의 gradient(local gradient)를 계산하는 것인데 Forward 단계에서 활성화 함수는 벡터 $ Z^l $의 각 원소마다 독립적으로 작용해 비선형 공간의 값으로 변환하는 벡터함수(Vector Function)다.

  • $A^{[2]}$ 의 각 원소 $A_i$는 입력 벡터의 원소 $Z_j$에 대해 $i \ne j$인 원소에는 영향을 받지 않는다.
  • 따라서 $i=j$ 일 때만 gradient $\frac{\partial f_i(x_i)}{\partial x_i} $ 가 발생한다.
  • 그 결과 $ \frac{\partial A^{[2]}}{\partial Z^{[2]}} $는 대각 행렬(Diagonal Matrix)이 된다.

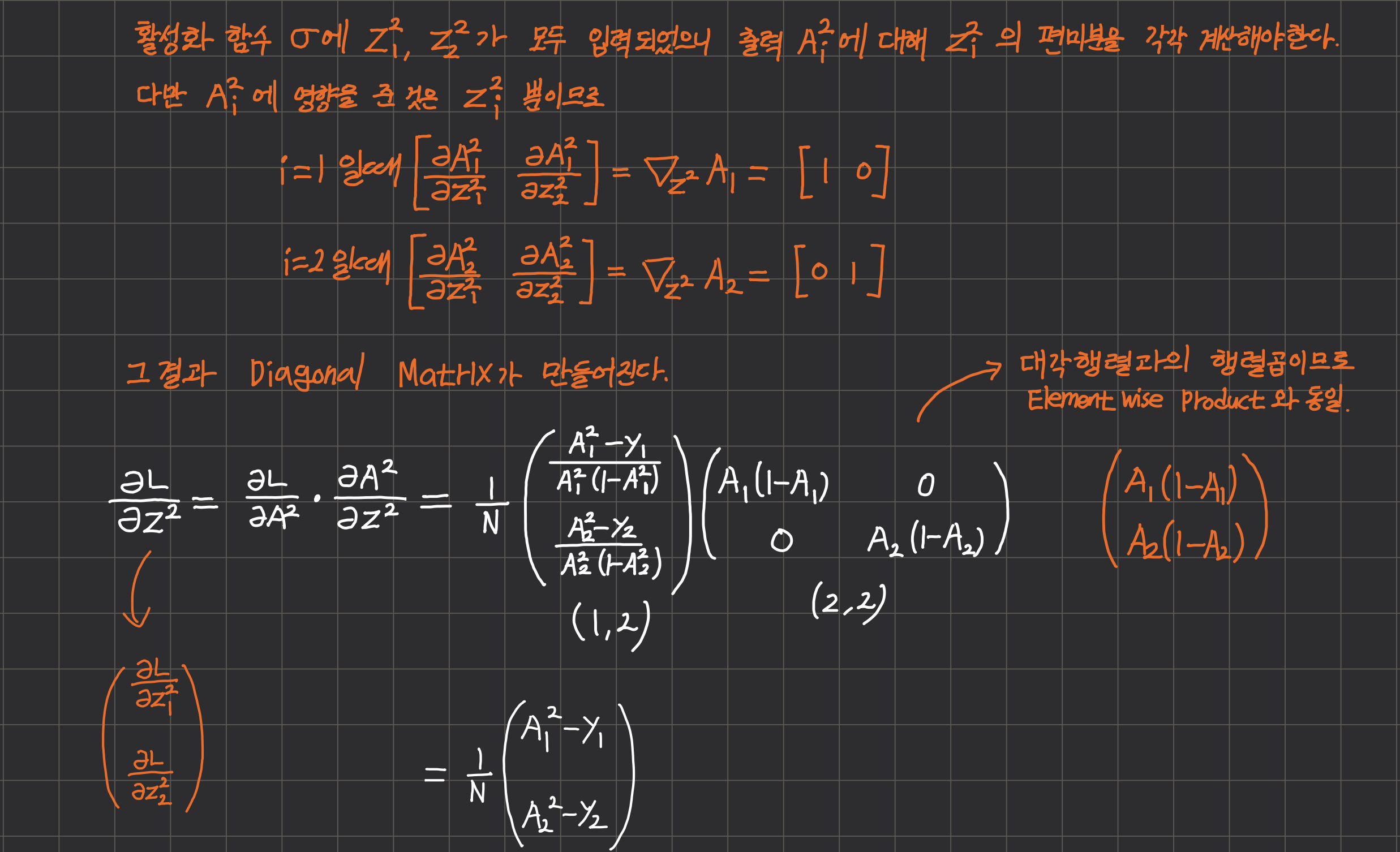
하지만 이런 식으로 접근하면 편미분을 원소로 하는 행렬을 구할 때나 chain rule을 계산할 때 너무 복잡해질 우려가 있기 때문에 0인 원소들을 제거하여 Sparse Matrix로 취급하자.

실제로 이 방식은 수학적으로 아무런 문제가 없다.
왜냐하면 $ \frac{\partial A^{[2]}}{\partial Z^{[2]}} $가 대각 행렬이라 chain rule에서 Upstream Gradient와 행렬곱(Matrix Multiplication)으로 계산한 결과와 원소곱(Element wise product)으로 계산한 결과가 같기 때문이다.

정리하면 Forward 단계에서 활성화 함수에 입력된 텐서의 형상과 Back-Prop 단계에서 활성화 함수에 대한 선형변환인 Local Gradient $ \frac{\partial A^{[l]}}{\partial Z^{[l]}} $ 는 형상이 같다.

다음으로 선형층이 보유한 학습파라미터를 업데이트할 gradient를 계산한다.
여기서도 도움이 될만한 팁이 있는데, 손실함수 값과 같은 Scalar에 대한 벡터나 행렬의 편미분 $\frac{\partial L}{A^{l-1}}, \frac{\partial L}{\partial W^l}$의 형상은 반드시 $A^{l-1}, W^l$과 같아야 한다.

계산과정을 정리해보면 다음과 같다.

  1. $\frac{\partial L}{\partial W^l}$의 형상은 $W^l$과 같아야 하므로 (3, 1) 행렬.
  2. 해당 행렬의 각 원소 $\frac{\partial L}{\partial W^l_{11}}, \frac{\partial L}{\partial W^l_{21}}, \frac{\partial L}{\partial W^l_{31}}$ 을 각각 계산.
  3. 2에서 계산한 값을 $\frac{\partial L}{\partial W^l}$에 대입하고 행렬곱의 형태로 분해(Decomposition)한다.

계산된 마지막 결과를 보면 ${A^1}^T \cdot \frac{\partial L}{\partial Z^2}$로 Local gradient인 $\frac{\partial Z^2}{\partial W^2}$의 결과가 선형변환 층의 입력인 $A^{l-1}$에 전치인 것을 알 수 있다.

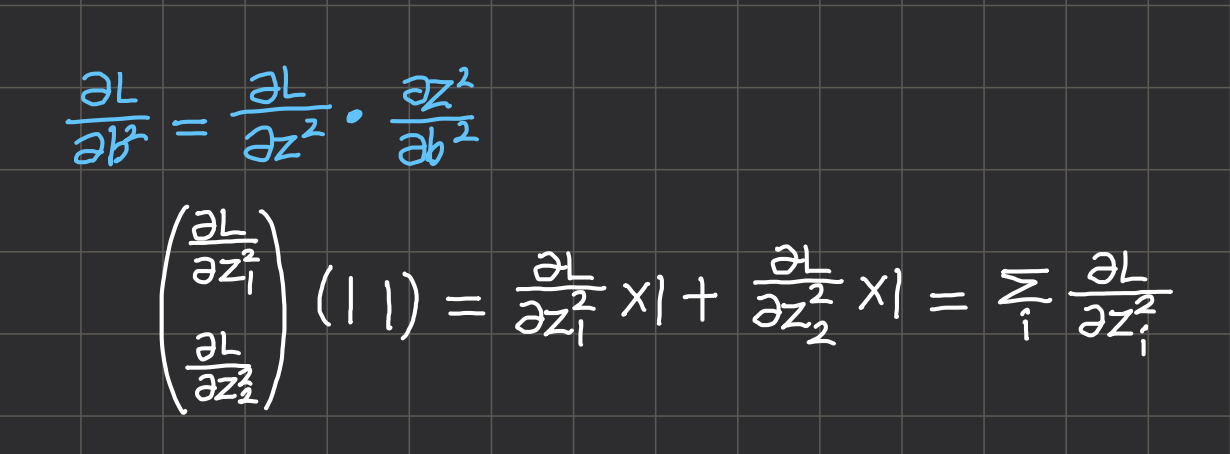
bias에 대해서는 계산이 정말 간단한데, $Z = {A^{l-1}}^TW + b $에서 b는 단순한 상수이기 때문에 편미분을 수행한 결과가 1이다. 따라서 $ \frac{\partial L}{\partial b^l} = \frac{\partial L}{\partial Z^l} \cdot 1 $이다.

마지막으로 {Z^l} 층의 입력 $A^{l-1}$의 gradient를 구한다. 여기서는 {W^l}에서 한 것과 마찬가지로 $\frac{\partial L}{\partial A^{l-1}}$의 형상이 $A^{l-1}$과 같음을 이용해 gradient 행렬을 먼저 정의하고, 각 원소들을 구한 뒤 행렬곱의 형태로 분해하면 된다. 결과를 보면 $\frac{\partial L}{\partial A^{l-1}} = \frac{\partial L}{\partial Z^l} \cdot {W^l}^T$로 $\frac{\partial Z^l}{\partial A^{l-1}}$이 ${Z^l}$의 weight에 대한 전치(Transpose)임을 볼 수 있다.

2.l-i번째 층의 gradient

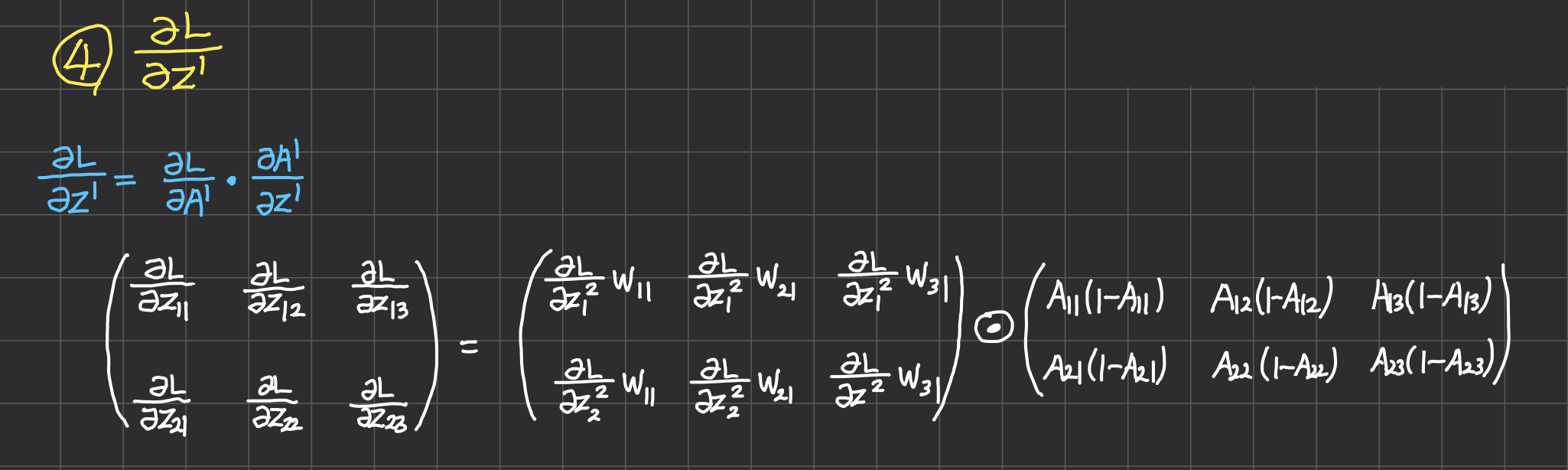
그 다음부터는 출력층에서 한 것과 똑같이 하면 된다.

  • $\frac{\partial L}{\partial Z^{l-1}} = \frac{\partial L}{\partial A^{l-1}} \cdot \frac{\partial A^{l-1}}{\partial Z^{l-1}} $을 계산한다.
  • 이 때 $ \frac{\partial A^{l-1}}{\partial Z^{l-1}} $의 형상은 활성화 함수의 입력 텐서 형상과 동일하다.
  • $\frac{\partial L}{\partial W^{l-1}}, \frac{\partial L}{\partial X} $의 형상은 $W^{l-1}, X$와 동일하다.

4.마치며

이번 정리를 통해 딥러닝에서 사용되는 신경망이 학습하는 원리에 대해 명확해질 수 있길 바란다. 앞서 말한대로 역전파는 딥러닝 프레임워크가 자동으로 계산하는 부분이기 때문에 개발자가 직접이를 구현할 필요는 없다. 다만 어떤 식으로 학습하는지 명확하게 알고 있어야만 학습과정에서 산출되는 손실값을 보고 학습이 어떤 상태인지, 어떤 문제를 가지고 있는지 해석이 가능하기 때문에 개념적인 부분만큼은 반드시 이해하고 넘어가야한다.(뇌피셜임)

댓글남기기

참고