CNN Base Models
CNN 기반의 모델들을 정리
1.VGG Net(2014)
(VGG(Very Deep Convolutional networks for Large Scale image recognition))[https://arxiv.org/abs/1409.1556] 논문은 CNN의 Depth 즉, convolution layer의 수를 증가시킴(NN의 depth가 증가)에 따른 성능의 향상을 보여준다.
핵심 내용은 모든 convolution layer에 필터의 크기가 $ 3 \times $로 설정되었다는 점인데 다음과 같은 특징들을 갖는다.
- 3개의 conv layer로 구성된 CNN 모델이 있다고 가정.
- 각각의 conv layer는 $ 3 \times 3 $의 필터를 사용.
- 따라서 첫번째 conv layer의 receptive field는 $ 3 \times 3 $이다.
- 두번째 층으로 전달되었을 때, 첫번째 층에서 $ 3 \times 3 $ 영역내 인접 픽셀들이 하나의 값으로 종합되었기 때문에 두번째 층은 총 $ 5 \times 5 $ 만큼의 영역을 한 번에 보는 것과 같다.
- 동일한 방식으로 세번째 층에서는 한 번에 $ 7 \times 7 $ 의 receptive field를 갖는다.
$ 7 \times 7 $ 필터를 갖는 conv layer 하나를 사용했을 때 파라미터가 $ 7 \times 7 \times N filters = 7^2C^2 $ 이고 $ 3 \times 3 $ 필터를 갖는 conv layer를 3개 사용했을 때 총 파라미터는 $ 3 \times (3 \times 3 \times N filters) $ 로 동일한 Receptive Field를 보유하면서 더 층을 깊게 만들 수 있고(비선형성을 높일 수 있음) 더 적은 파라미터를 사용하게 된다.

논문에서 공개한 모델의 상세 구조를 봤을 때 모델이 굉장히 간단하게 구성되었음을 알 수 있고, 이러한 구조 및 설정들은 이후 발표되는 모델에서도 많이 사용하고 있을 만큼 효과적이다. 하지만 Decoder(Classifier)가 Fully Connected Layer들로 구성되어 있기 때문에 파라미터 수가 많아지고, 속도 역시 느린 편이다.
2. ResNet(2015)
(ResNet(Deep Residual Learning for Image Recognition))[https://arxiv.org/abs/1512.03385]의 내용은 VGG 보다 훨씬 깊게 모델을 쌓기 위해 연구를 수행하였고, Skip Connection이라는 새로운 개념을 통해 100층 이상의 매우 깊은 모델을 만들어내는데 성공하였다.
2-1.문제점 - Degradation

흔히 Bias-Variance Tradeoff라는 개념은 모델의 복잡도(Complexity) 즉, 파라미터의 수가 너무 많아지면 train data에 모델이 과적합되어 test data와 같은 unseened data에 대한 예측 성능이 낮아지고 모델의 복잡도가 너무 낮아지면 train data에 대해서도 제대로 학습하지 못해 train error가 높아지기 때문에 적절한 복잡도를 찾아내야 함을 말한다.
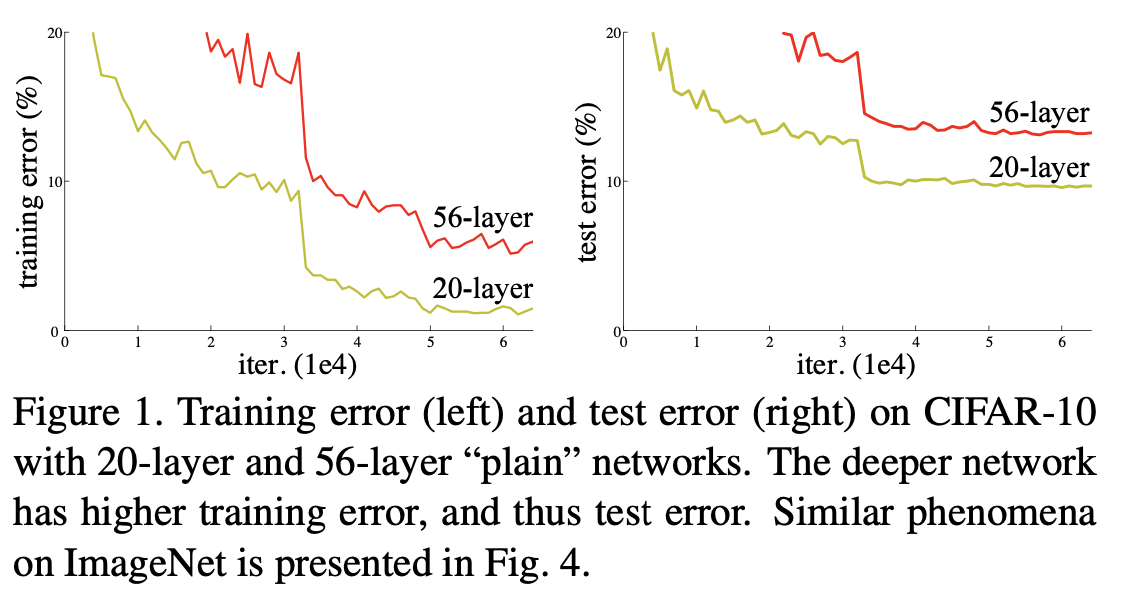
이를 기반으로 논문에서는 20개 층으로 구성된 모델 A와 56개 층으로 구성된 모델 B를 학습시켰을 때의 결과를 그래프로 보여주고 있다.
- 이 그래프에서 눈여겨 봐야할 점은 왼쪽, training error에 대한 그래프인데 앞서 bias-variance tradeoff에 따르면 모델의 depth가 깊어질수록 training error는 더 크게 감소해야하고 test error가 더 높은 양상을 보이는 것이 타당할 것이다.
- 하지만 오히려 더 깊은 모델의 training error가 얕은(Shallow)모델 보다 더 높은 결과를 보여주며 Overfitting이 아닌 또 다른 문제에 빠졌음을 말한다.
- 논문에서는 이렇게 “깊이의 증가에 따른 학습 성능 저하” 문제를
Degradation이라 정의한다.
2-2.해결책 - Skip Connection
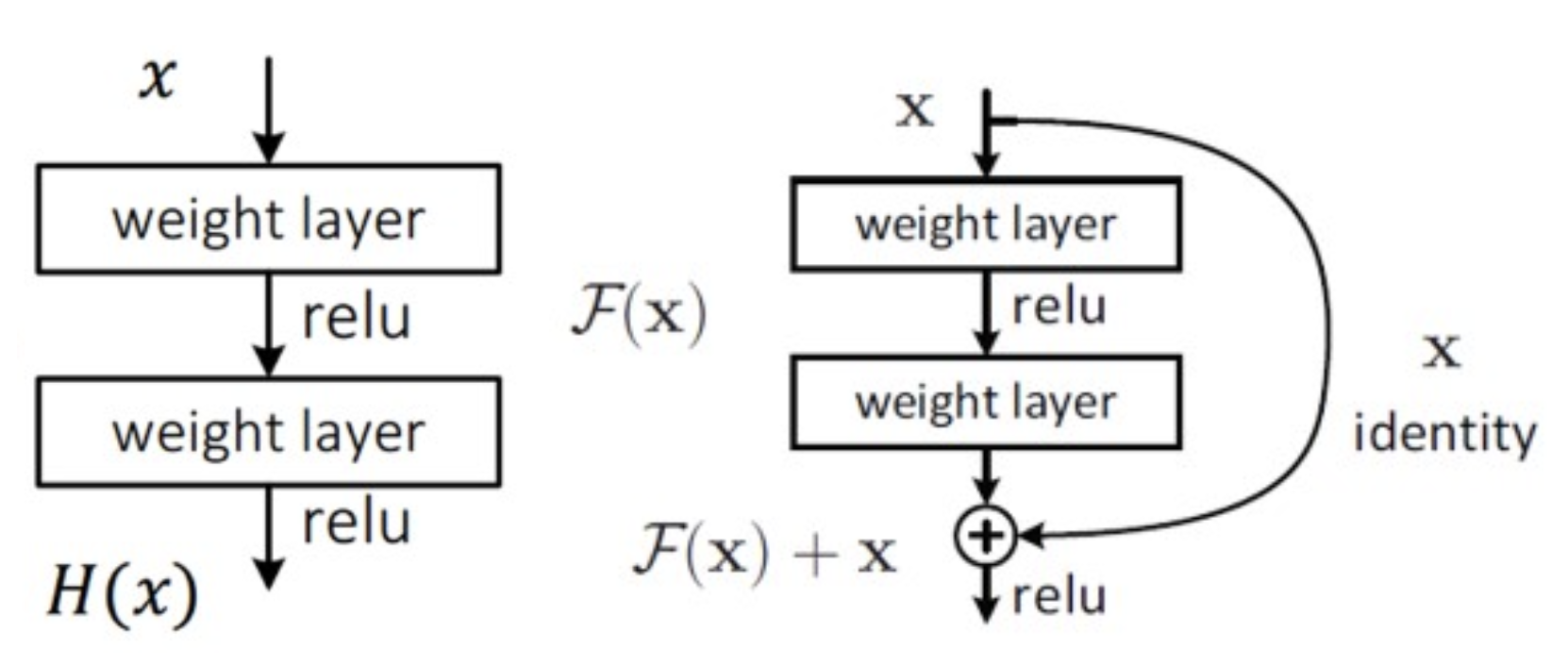
왜 Degradation 문제가 발생했는지부터 이해하기 위해 왼쪽 그림을 보자.
이는 우리가 지금까지 흔히 봐왔던 전형적인 DNN의 블록이며 논문에선 이를 Underlying Mapping이라 부르고 있다.
- 입력 $x$가 주어진 함수(블록) $F$를 통과했을 때의 결과를 F(x)라고 한다.
- 손실함수의 값을 최소값으로 만들기 위한 함수의 출력이 $H(x)$라고 가정하자.
- 따라서 해당 함수는 $F(x)=H(x)$가 되도록 학습을 하는 것이 이상적이다.
- 하지만 모델의 깊이가 굉장히 깊다면, 그만큼 함수 자체가 보유하고 있는 변수(trainable parameters)가 굉장히 많을텐데 문제는 $F(x)=H(x)$로 만들기 위해 많은 수의 파라미터를 조정하기가 너무 어렵다는 것이다.
적절한지는 모르겠지만 나는 이것을 “네비게이션이나 지도 없이 서울에서 출발해 부산으로 도착하라는 것과 같다.”라고 비유한다.
이제 문제의 해결책인 Skip-connection이 도입된 오른쪽 블록을 보자.
skip-connection 자체는 굉장히 단순한데, 해당 블록의 입력 $x$를 마지막 층의 출력 $F(x)$에 더해 $F(x)+x$를 구하고 Activation function을 적용하면 끝이다. 너무나도 간단한데 왜 이것이 열쇠가 되었을까??
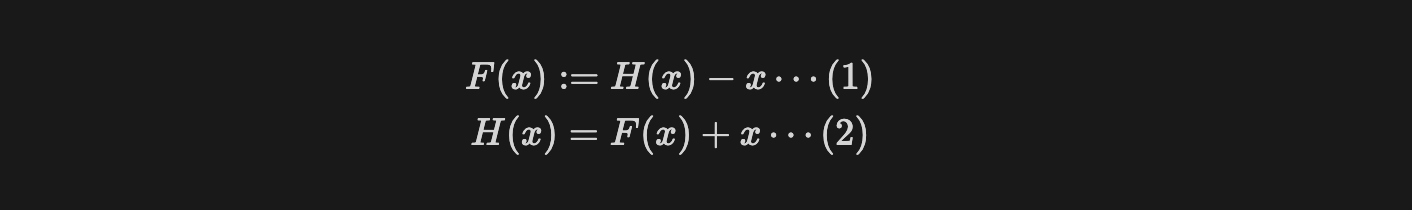
- skip connection의 도입으로 함수(블록) $F$는 식(1) $ F(x):=H(x)-x $이 되었다.
- 이는 이상적인 출력값 $ H(x) $와 입력값 $ x $간 차이(잔차, Residual)를 구하도록 함수 F가 갖는 파라미터를 조정하라는 것으로 문제가 바뀌었음을 의미한다.
- 더 자세히 해석하자면 식(1)은 $F$는 $ H(x) \approx x $가 되어 $ F(x) \approx 0 $이 되어야 함을 의미한다.
1번, 2번까지는 알겠는데 3번은 뜬금없이 뭘까?
깊은 모델은 $x$가 입력층부터 출력층까지 이동하면서 많은 양의 선형변환 + Activation이 적용될 것이기 때문에 변화량이 많을 것이다. 쉽게 말해 출력층에 가까워질수록 필요한 정보만 남겨놓기 때문에 수차례 변화된 값을 입력으로 받게 된다. Ehgks $F(x)=H(x)$를 달성하기 위해 특정 블록에서 굉장히 크게 입력을 변화시켰다면 나머지 블록들은 큰 변화에 매번 적응해서 $F(x)=H(x)$를 이루어야만 한다.
따라서 skip connection, 함수 $F$가 $ $ F(x):=H(x)-x $로 H(x) \approx x 가 되도록 하는 것은 블록의 출력이 입력과 근사할만큼 `조금씩 바꾸자라는 것으로 해석된다. 조금씩만 바꿔도 앞으로 통과해야하는 층이 많기 때문이다. 또한 모델이 이상적으로 학습되었다면 함수의 출력 $F(x)$는 0에 근사하게 될텐데 이는 weight matrix가 영행렬에 근사함을 의미하고, Weight Initailization 방법들 역시 평균을 0으로 하고 있기 때문에 학습으로 조정해야할 파라미터 변화량도 크지 않아 학습이 쉽게 이루어질 수 있게 된다.
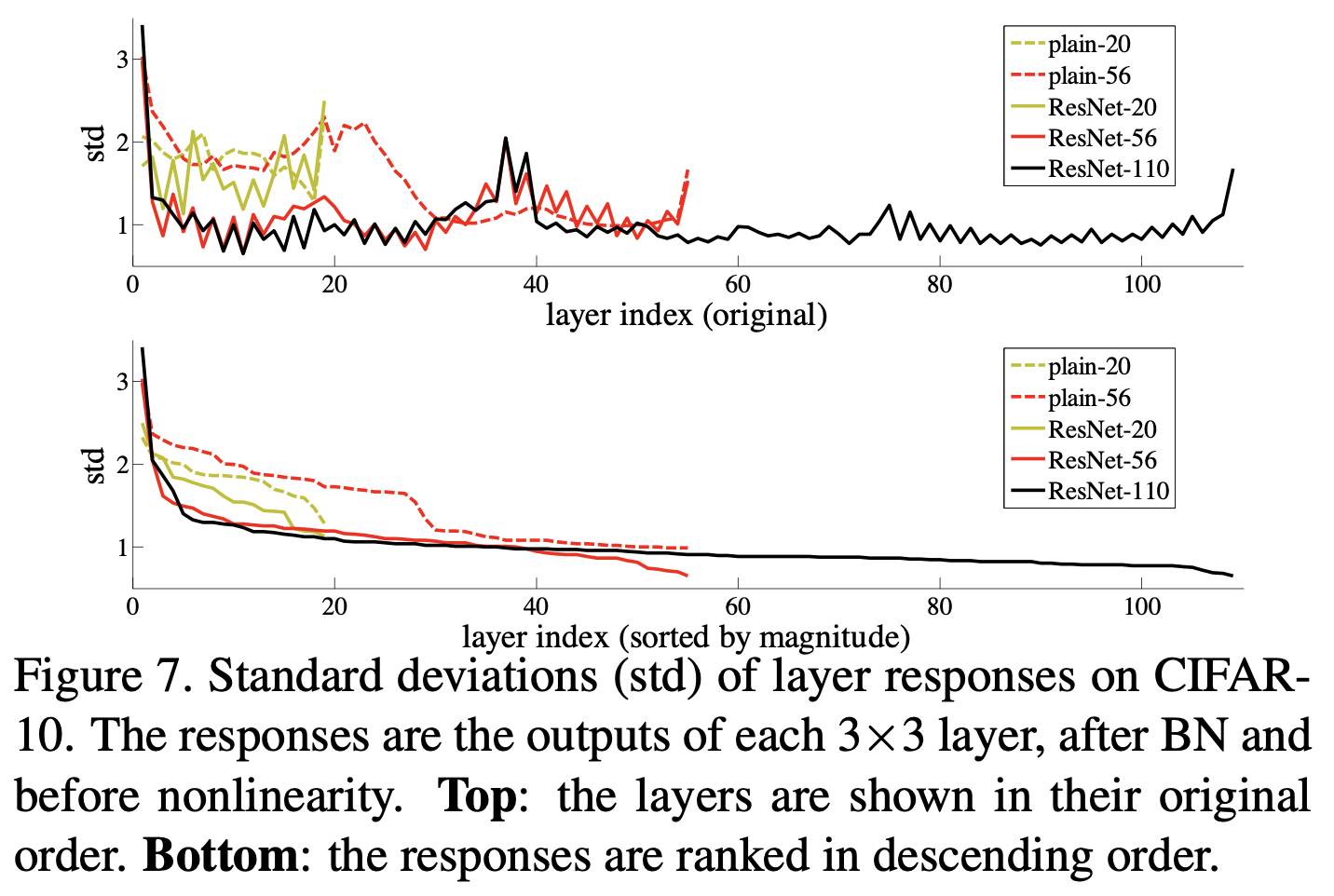
논문에서는 이러한 방법들이 의도한대로 동작하는지 확인하기 위해 다음과 같은 그래프를 첨부했다.
Layer responses는 신경망의 특정 층(layer)이 입력에 대해 생성하는 출력값을 의미하는데 Skip connection이 적용된 모델은 층이 깊어짐에도 불구하고 출력값의 분산이 작은 것을 확인할 수 있다.
2-3.Basic Block, Bottleneck Block
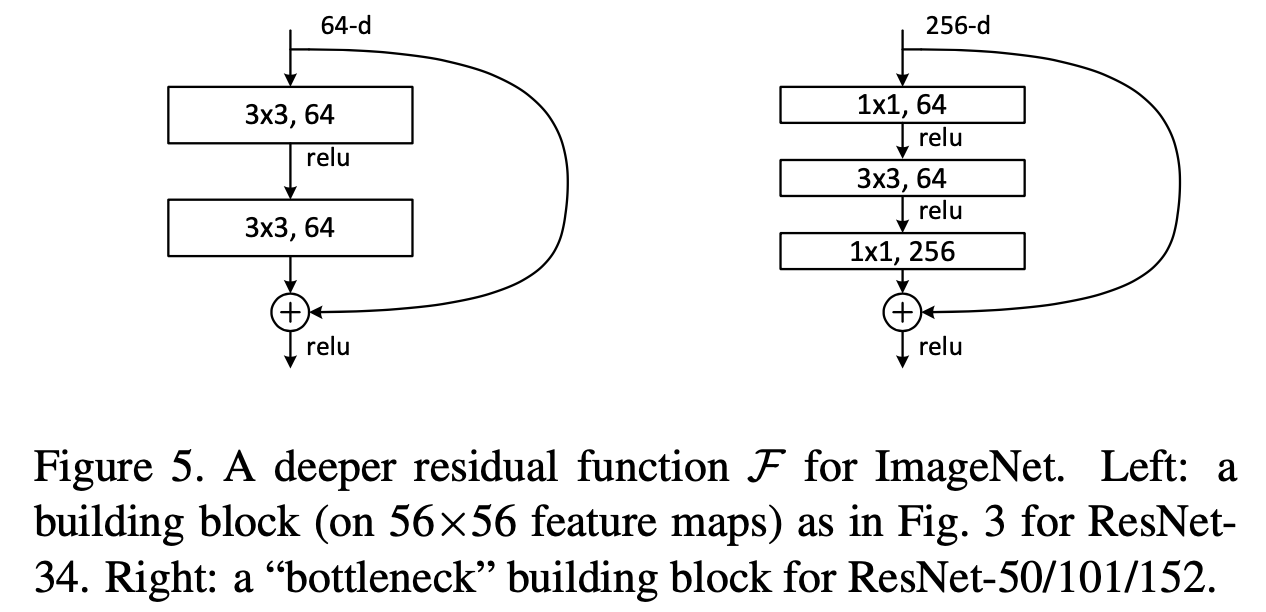
ResNet을 구성하는 블록은 두 가지인데 ResNet18, 34에는 Basic Block(왼쪽)이 적용되고 50, 101, 152에서는 Bottleneck Block(오른쪽)이 적용된다.
- BasicBlock은 Underlying Mapping 구조에서 skip connection이 추가된 구조.
- BottleNeck Block은 먼저 $ 1 \times 1 $ 컨볼루션 층을 통해 입력의 차원(256dim)을 줄여주고(64dim) 이를 $ 3\times 3 $ 컨볼루션 층에 입력하여 spatial information을 추출한다. 이후 다시 $ 1 \times 1 $ 컨볼루션을 이용해 최초 입력의 차원(256dim)으로 늘린 후 skip connection을 수행한다.
BottleNeck이라는 용어가 앞으로 공부하면서 굉장히 자주 등장할텐데 이는 채널이 큰 텐서를 $ 1 \times 1 $ 컨볼루션을 통해 채널의 크기를 줄여주는 형태를 말한다.
3.MobileNetV2(2018)
(MobileNetV2: Inverted Residuals and Linear Bottlenecks)[https://arxiv.org/abs/1801.04381]
이 모델은 전작인 MobileNetV1에서 발전된 것인데 V1, V2은 모두 “ResNet 이후 모델의 크기를 증가시켜 성능을 높히는 것에 과몰입하는 문제가 있으며 edge device 같은 한정된 계산 자원을 가졌다면 적용이 불가능할 것”이라는 문제점을 제시하며 성능적인 손실이 없으면서 edge device에 적용될 수 있을 정도로 경량화할 수 있음을 제시한다.
3-1.Inverted Residual Block
본 논문에서는 Inverted Residual Block이라는 새로운 block 구조를 제안하는데 우선 일반적인 Residual Block을 다시 한 번 보자.
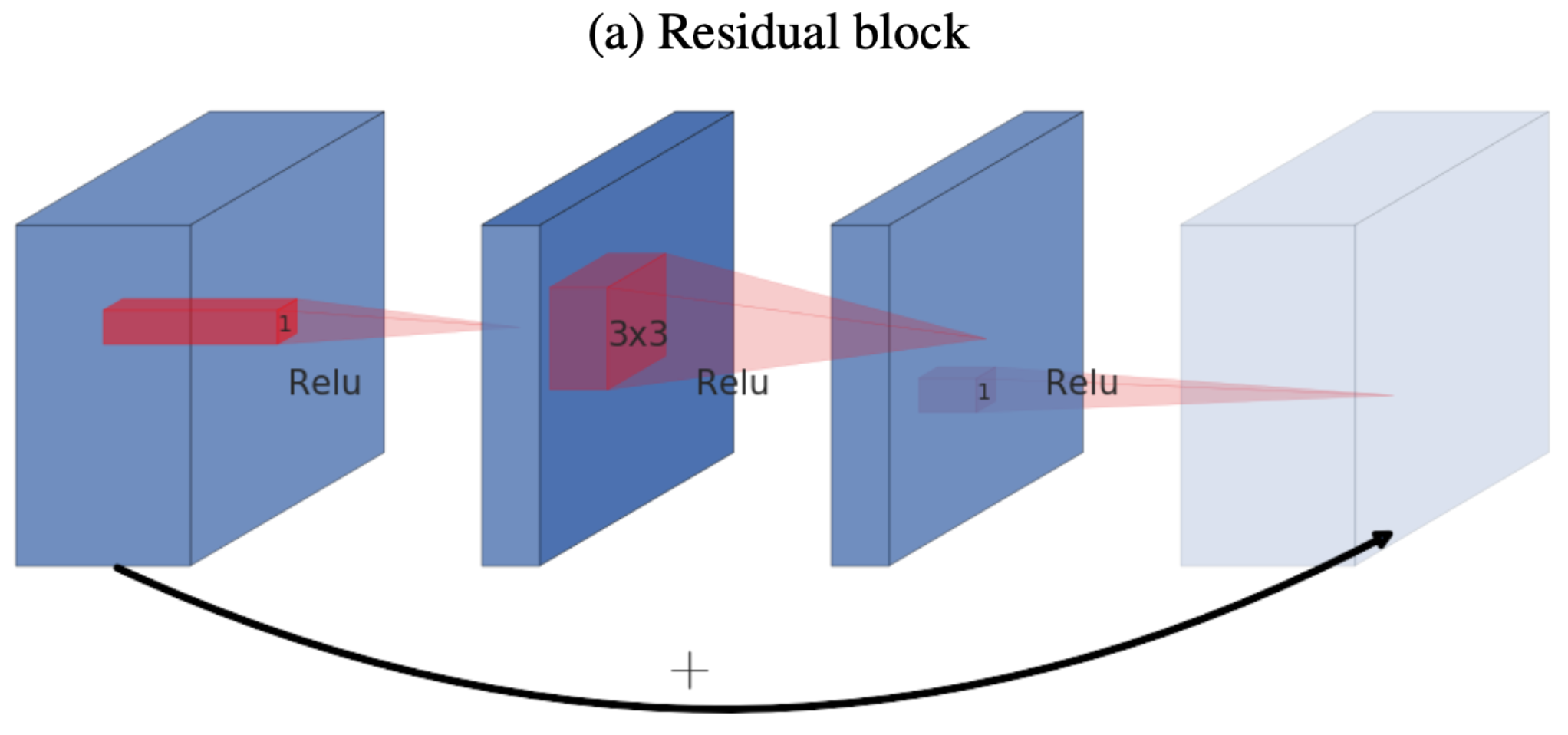
- 일반적인 Residual Block은
wide→narrow→wide형태로 구성된다. - 블록으로 입력되는 텐서가 256차원이라고 가정.
- 첫번째 층인 $1\times 1$ conv + ReLU를 통해 차원의 수를 줄이는 Bottleneck역할을 한다.(Wide → Narrow)
- 두번째 층 $3\times 3$ convolution + ReLU에서는 채널 수를 높인 expansion 상태에서 receptive field를 증가시킴으로써 정밀한 feature를 포착하려고 한다.
- Skip-Connection(Element-wise Addition)을 수행하기 위해 64차원을 256차원으로 조정해야한다.
- 따라서 세번째 층인 $1\times 1$을 적용해 차원의 수를 늘리는 Expansion역할을 한다.(Narrow → Wide)

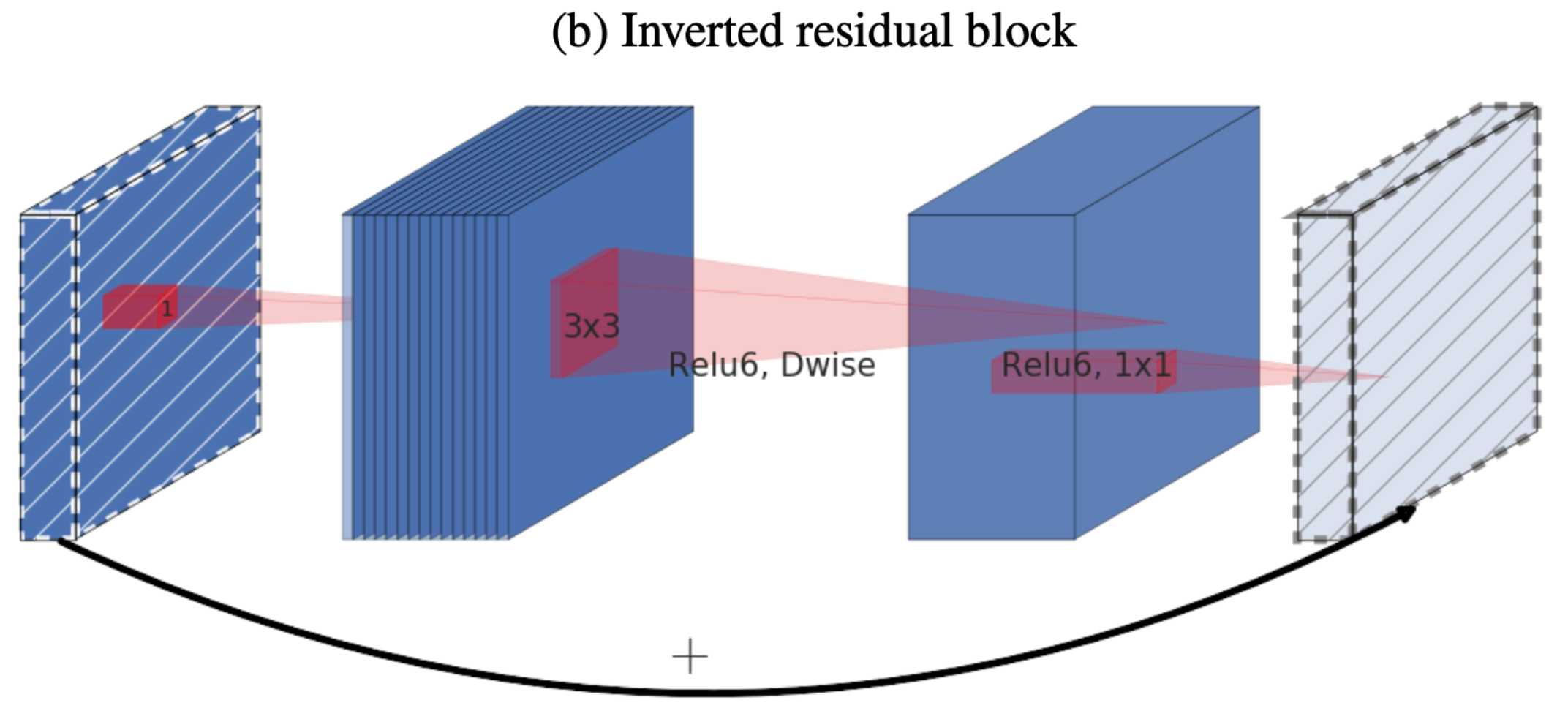
Inverted Residual Block은 이름에서 알 수 있듯이 Residual Block의 역구조라는 것을 알 수 있다.
- Residual block과 반대로
narrow → wide → narrow로 구성된다. - 입력된 텐서가 64차원이라 할 때, 첫번째 층인 $1\times 1$ conv + ReLU6를 통해 256차원으로 늘리는 Expansion역할을 수행한다.(narrow → Wide)
- 두번째 층 $3\times 3$ Depthwise convolution + ReLU6
- 세번째 층인 $1\times 1$을 적용해 256차원을 64차원으로 다시 줄이고(Wide → Narrow) Skip-Connection을 수행한다.
간단하게 정리하면 낮은 차원의 입력을 잠시 높혀서 특징을 추출하고 난 뒤 다시 채널을 낮춰서 다음 층으로 전달하는 block들로 모델을 구성함으로써 전체적인 파라미터 수를 감소시킬 수 있게 한다.
한 가지 특이점은 세번째 층에서는 Activation function을 적용하지 않는데 이에 따라 논문에서는 세번째 층을 Linear BottleNeck이라 소개한다.
두 개의 그래프는 Inverted Residual Block의 Bottleneck layer에서 non-linearity function의 유무에 따른 성능 차이와 Shortcut connection의 위치에 따른 성능 차이를 비교하여 보여주고 있다.
- 왼쪽 그래프는 activation function이 적용되었을 때(초록색)와 적용되지 않았을 때(파란색)의 성능을 비교한 것인데, Linear Bottleneck이 ReLU6를 bottleneck에 적용했을 때 보다 더 좋은 성능을 보인다.
- 오른쪽 그래프는 Shortcut connection을 Linear bottleneck의 출력에 연결했을 때(파란색)와 expansion의 출력에 연결했을 때(초록색), 그리고 shortcut connection을 적용하지 않았을 때(빨간색)의 결과를 보여주며, linear bottleneck의 출력에 연결했을 때 가장 좋은 성능을 보인다.
3-2.Manifold of Interest
Inverted Residual Block은 Residual Block보다 파라미터 수가 더 적은데 어떻게 성능적인 손실이 없을 수 있을까?? 논문에서는 이를 Manifold of Interest 가정을 기반으로 의문에 대답한다.
- Manifold는 고차원에 해당하는 데이터가 가진 저차원의 특징(feature)을 말한다.
- 이미지는 수많은 픽셀들로 이루어진 매우 고차원의 공간에 존재하지만 실제로 유용한 정보를 담고 있는 특징은 보다 낮은 차원에 존재할 것이다.
- Manifold of Interest는 고차원 공간에 존재하는 값이 내재하고 있는 핵심적인 저차원의 feature를 학습할 수 있다는 가정으로, Inverted Residual Block과 같이 narrow → wide → narrow 형식의 연산을 하더라도 문제가 없으며, 계산적으로 훨씬 효율적이라는 주장이다.

실제로 이 가정에 대해서도 실험한 결과를 제시하는데 핵심은 저차원 공간에 있던 값의 분포가 고차원 공간에 mapping되었다가 다시 저차원으로 projection되었을 때, 원래의 분포가 얼마나 유지되는가이다.
- 가장 왼쪽의 나선형 그래프는 입력의 분포.
- (왼쪽에서 오른쪽으로) 차원을 점차 증가(Expansion) 시키면서, 다시 원래의 차원으로 감소(BottleNeck)시켰을 때의 분포를 다시 그래프로 그린다.
- 실험 결과를 보면 expansion으로 증가시키는 차원이 높을수록 원래의 차원으로 줄였을 때 원래의 분포가 더 많이 유지되는 것을 볼 수 있다.
- 쉽게 말해 narrow → wide 단계에서 늘리는 차원의 크기가 커야 한다는 것이다.
3-3.ReLU6

ReLU6는 ReLU 함수와 거의 같지만, 입력값이 6보다 큰 경우 6으로 고정하여 반환하는 비선형 함수이다.
논문에서는 ReLU6가 INT8이나 FP16과 같은 low-precision 연산에 강건(Robust)하다는 특성이 있기 때문에, 모바일 같은 Edge device에서 ReLU보다 더 효과적이라고 한다.
- 여기서 low-precision이라는 것은 “정밀도가 낮은 연산”임을 의미한다.
- INT8이나 FP16은 각각 8비트를 사용해 정수, 16비트를 이용해 부동소수점을 나타냄을 의미한다.
- 일반적으로 딥러닝 프레임워크에서는 FP32 즉, 32비트 실수 연산을 기반으로 연산이 수행되기 때문에 INT8이나 FP16은 사용 가능한 숫자의 범위가 더 좁은, 제한적인 셈이다.
- 이에 따라 ReLU6는 FP32보다 FP16, INT8로 precision을 낮췄을 때 적합하며 컴퓨팅 자원을 더 적게 사용할 수 있게 된다.
4.EfficientNet(2019)
(EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks)[https://arxiv.org/abs/1905.11946]
논문에서 제시하는 문제점은 “최근까지 연구된 모델들은 Depth나 Width 또는 Input Resolution을 증가시키기만 하여 성능 개선을 도모했다.”로 보다 효과적인 모델의 Scale Up 방식은 width, depth, resolution을 모두 적절하게 조절하여 모델을 설계하는 것임을 제시한다.
4-1.Width, Depth, Resolution
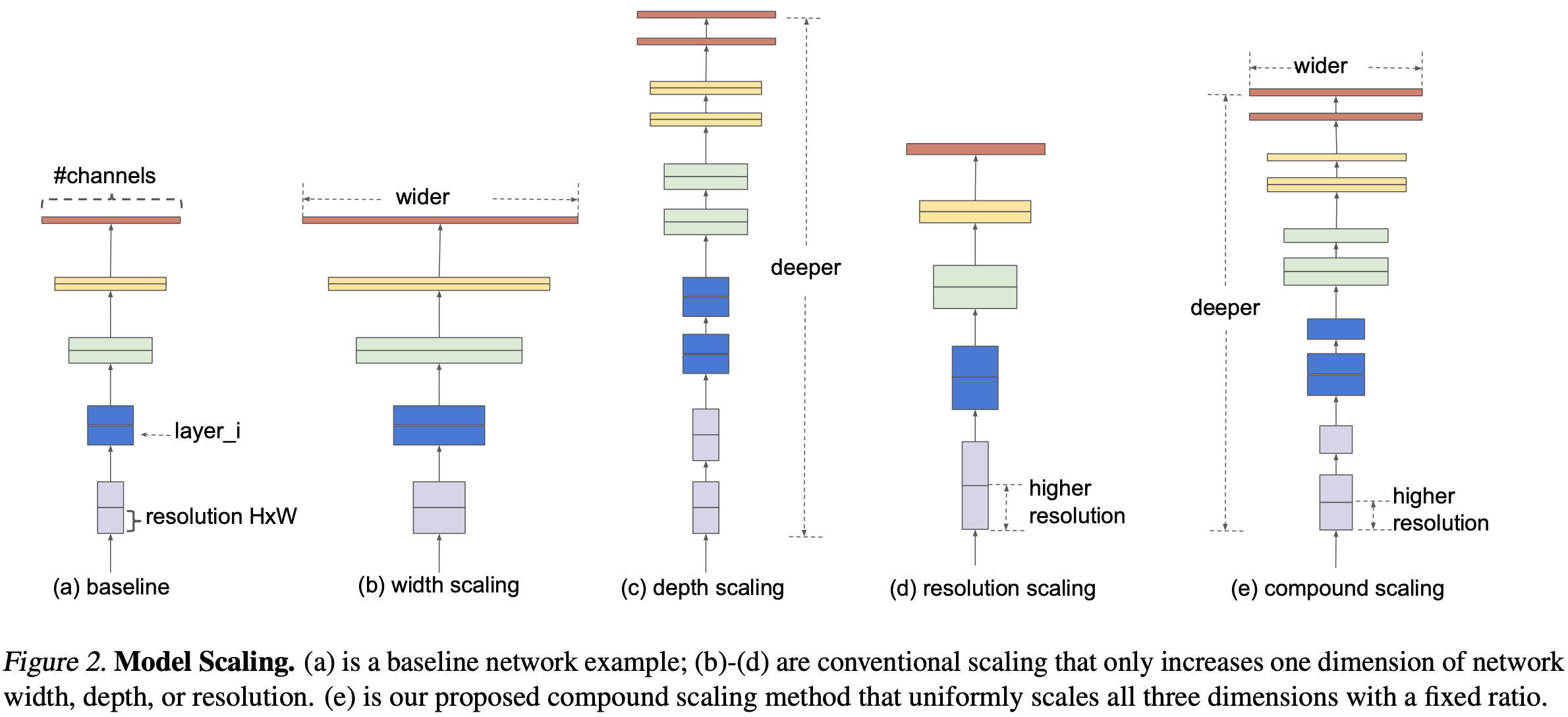
DNN을 설계할 때는 Width, Depth, Resolution을 조절하게 되는데 논문에서는 이를 Model Scaling이라고 한다.
Width Scaling
- Linear Layer 또는 Convolution layer와 같이 trainable parameter를 갖는 층은 설정하는 channel의 크기(뉴런, 필터의 수)에 따라 더 많은 parameter를 보유하게 된다.
- 학습 가능한 파라미터의 수가 많다는 것은 그만큼 데이터가 가진 복잡한 특성에 대해 학습이 가능하게 만들지만, 모델의 복잡도가 높아져 Overfitting될 우려가 있다.
Depth Scaling
- 모델을 구성하는 Layer 수를 조절한다.
- 더 많은 층을 통과할수록 비선형성이 높아져 복잡한 특성을 학습할 수 있다.
- 결과적으로 feature-level이 높아져 모델이 데이터 전체 맥락(Contextual Information)을 볼 수 있게 된다.
- 층 수를 늘릴수록 파라미터 수가 증가하여 모델 복잡도가 증가한다.
Input Resolution Scaling
- 입력 이미지의 해상도가 높아지면 더 많은 수의 픽셀을 갖게 된다.
- 즉, 더 많은 데이터 값을 포함하고 있기 때문에 모델이 학습할 특징이 더 많아지고 표현력이 더 풍부해진다.
- 해상도가 높아지는 것은 픽셀의 수가 증가하는 것과 같기 때문에 데이터 하나하나가 메모리 공간을 더 많이 차지하게 된다.
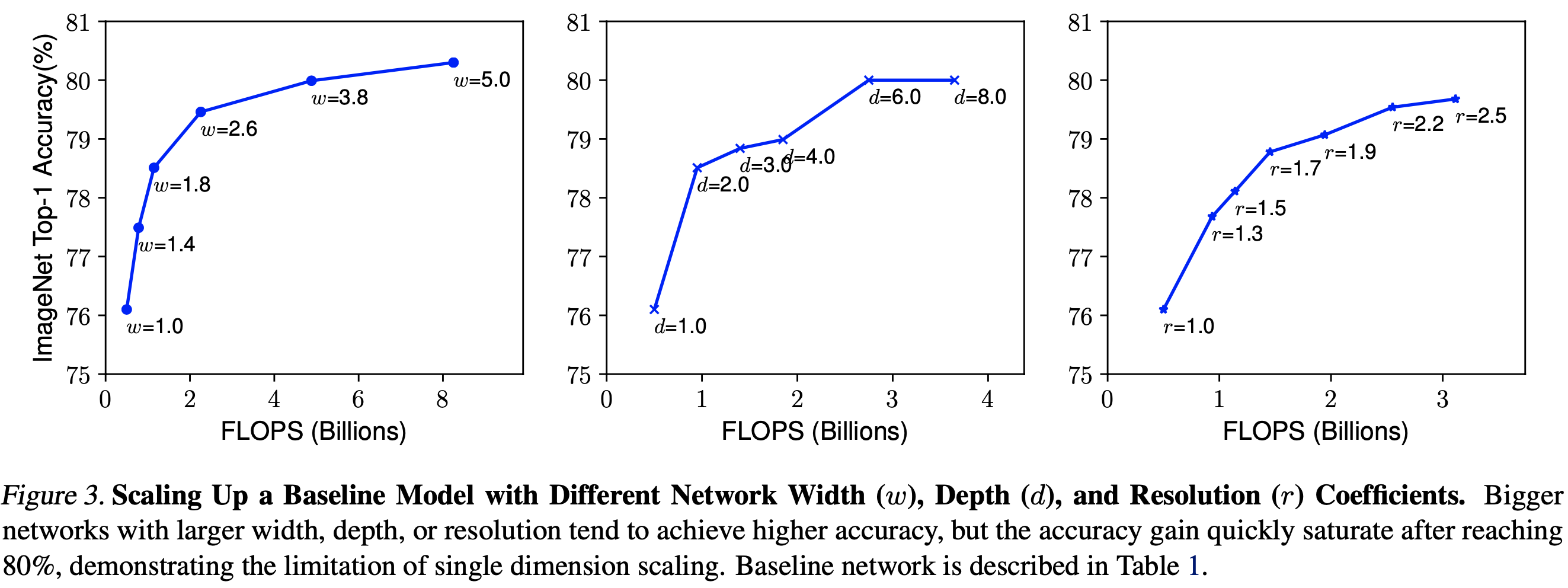
논문에서는 최근 연구들이 이러한 Scale Factor들을 모두 조절하는 것이 아니라 하나의 factor에 집중하는 연구 방식에 문제를 제시한다. 실제로 각각의 factor만을 증가시켰을 때의 성능을 그래프로 시각화하여 첨부하는데
- 왼쪽에서부터 width, depth, resolution.
- 어떤 Baseline Model을 기반으로, 3가지 요소 중 하나만 변화시켰을 때의 성능 지표를 나타낸 것으로, 변화 대상을 제외한 나머지 두 요소는 고정한다.
- width와 depth의 증가는 정확도가 빠르게 포화(Saturate)되는 형태를 보여준다. 즉, 설정 값을 계속 증가 시켜도 어느 정도의 개선이 이루어지고나면 더 이상 성능이 나아지지 않는다.
- resolution은 그나마 포화 양상이 적게 나타났다.
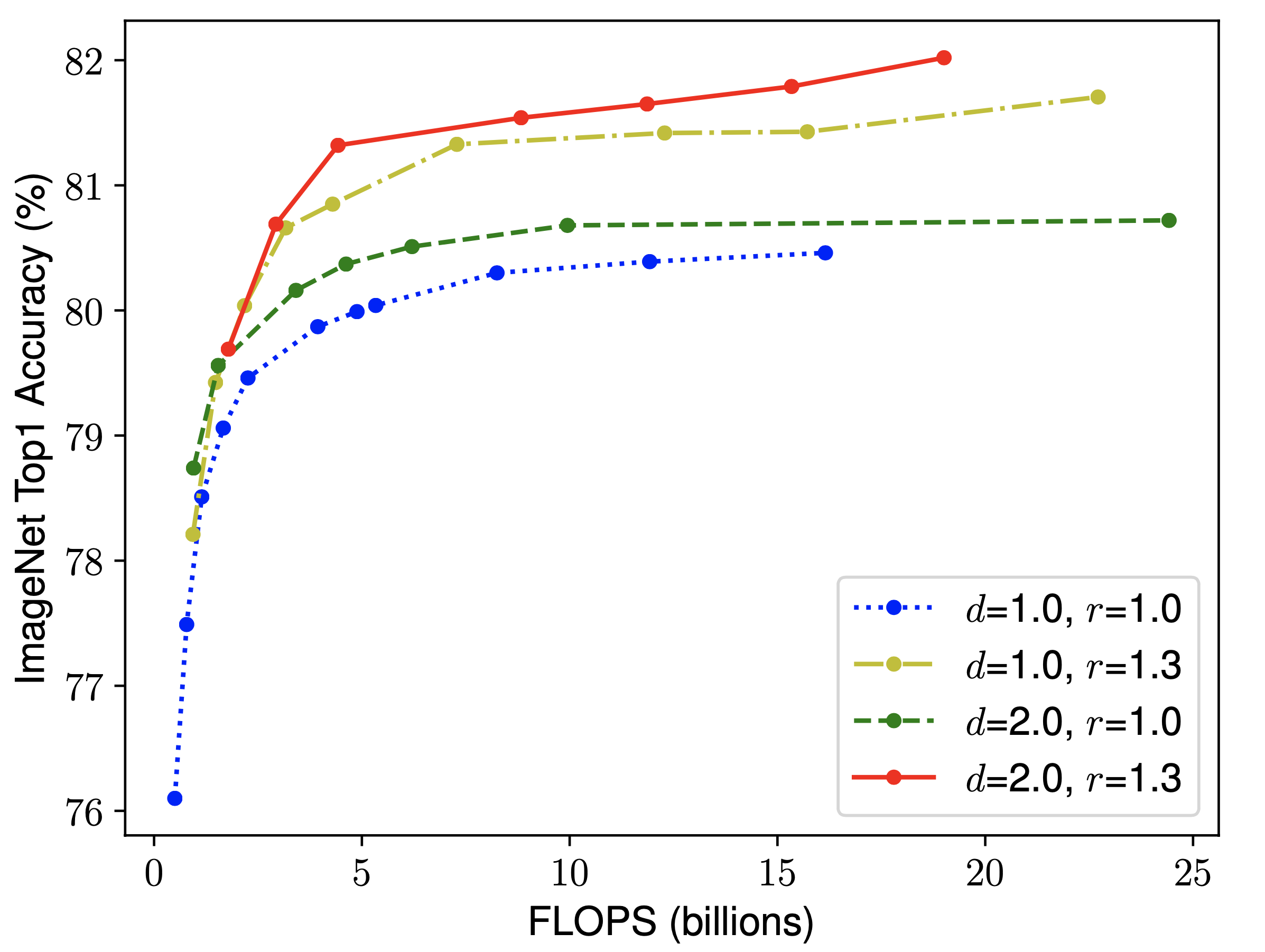
두번째 실험에서는 depth $d$와 resolution $r$을 특정한 값으로 고정시켜두고, width의 변화에 따른 정확도의 변화를 측정한다.
- 초록색$(d=2.0, \ r=1.0)$ 그래프와 노란색 $(d=1.0, r=1.3)$ 그래프를 비교해보면 depth의 증가보다는 resolution의 증가가 더 효과적으로 보인다.
- 빨간색 그래프와 나머지 3개의 그래프를 비교해보면, depth, width, resolution 3가지 요소를 모두 증가시켰을 때 가장 좋은 성능을 보임을 알 수 있다.
- 입력 이미지의 해상도가 커짐에 따라 픽셀 수가 더 많아졌다.
- 이에 따라 모델은 더 넓은 범위를 볼 수 있어야하며, depth의 증가에 따라 Receptive Field도 점점 커진다.
- 픽셀 수가 증가함에 따라 더 복잡하고 구체적인 특징이 데이터에 내제되어 있을 것이며, 이를 파악하기 위해 각 층의 width, trainable parameter의 수가 증가해야한다.
- 종합해보면 3가지 요소는 결국 연관되어 있음을 알 수 있다.
4-2.Compound Scaling
앞서 본 두 개의 실험을 통해 depth, width, resolution 3가지 요소를 함께 증가시키는 것이 가장 효과가 좋다는 것은 알게 되었지만, 아직 이들을 어떻게 설정해야할지 구체적인 방법이 없다.
논문에서는 3가지 요소간 최적의 비율이 있을 것이며, 이것을 계산하는 Compound Scaling이라는 체계적인 방법을 제시한다.
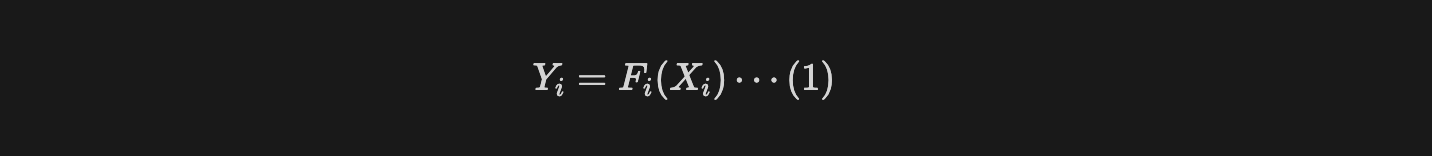
기본적인 layer를 수학적으로 일반화하면 (1)과 같은 식을 정의할 수 있다.
- $F_i$ : 연산자(operator, layer)
- $Y_i$ : 출력 텐서
- $X_i$ : $[H_i, W_i,C_i]$ 형상인 입력 텐서
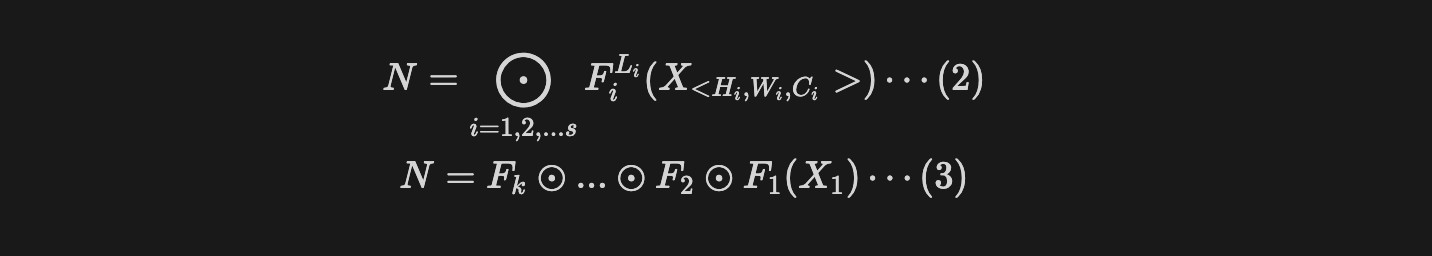
모델은 여러 개의 layer를 쌓아서 만들어지므로, 식(2) 또는 (3)으로 표현이 가능하다.
- $N$ : 다수의 stage들로 구성된 모델.
- $s$ : 모델을 구성하는 stage의 수.
- $F_i^{L_i}$ : i번째 stage를 구성하는 layer $F_i$.
- $L_i$ : i번째 stage에서 특정 layer $F_i$가 반복되는 수.
(2), (3)을 기반으로 다음과 같은 구체적 목표를 설정한다.
- 새로운 구조를 탐색하지 않고, Baseline이 되는 모델을 하나 선택한다.
- baseline 모델을 기반으로 width, depth, resolution을 체계적으로 확장해 가장 높은 정확도를 구한다.
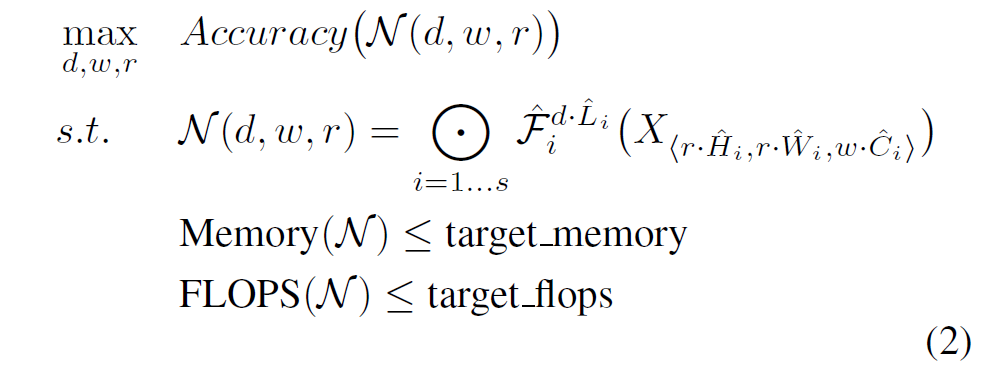
두 개의 식은 baseline Model $N$을 기반으로 $d, w,r$을 조정하여 가장 좋은 성능을 구함을 나타낸다.
- Depth : $\hat L_i$
- Width : $\hat C_i$
- Resolution : $(\hat H_i, \hat W_i)$
- 각각의 layer 마다 최적의 $\hat L_i, \hat C_i, \hat H_i, \hat W_i$를 탐색하기에는 범위가 너무 넓기 때문에 layer 마다 균일한 scaling을 적용한다.
- 이 때, baseline model을 성능이 좋은 것으로 선정하는 것이 중요하다고 한다. 아무리 최적의 비율을 찾아 적용하더라도 baseline model의 성능이 낮다면, 최고 정확도의 임계점이 낮기 때문.
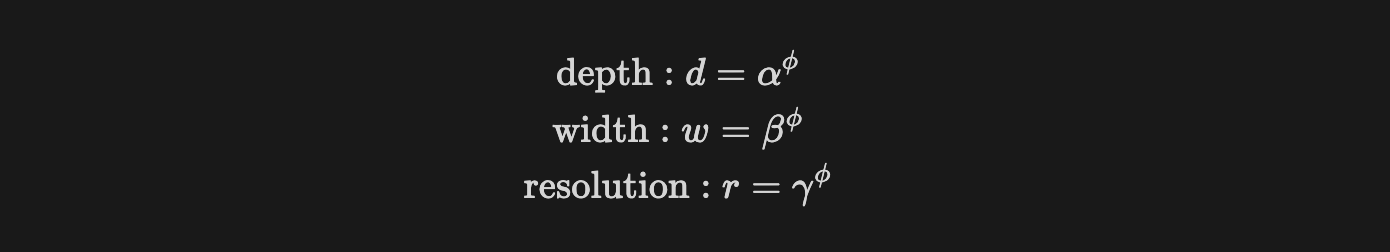
- depth, width, resolution을 각각 $\alpha, \beta, \gamma$로 나타낸다.
- $\phi$는 사용 가능한 리소스의 양으로, 사용자가 지정하는 계수이며 $\alpha, \beta, \gamma$에 모두 $\phi$가 있으므로, $\phi$를 통해 3가지 항목을 동시에 조절한다.
- $\alpha, \beta, \gamma$는 두 가지 전제 조건을 지켜야한다.
- $\alpha \geq 1, \ \beta \geq 1 , \ \gamma\geq 1$ → depth, width, resolution은 모두 1 이상의 실수여야한다.
- $\alpha \cdot \beta^2\cdot \gamma^2 \approx 2$ → 3개의 요소값을 곱한 결과값은 2에 근사해야한다.
- depth는 2배 증가시키면 FLOPS도 동일하게 2배 증가.
- width와 resolution에 제곱이 적용된 이유 : resolution은 가로, 세로에 각각 곱해지기 때문에 제곱만큼 증가하며 width는 층별로 필터 수(뉴런 수)를 증가시키면 output feature map의 채널도 증가하기 때문.
- 첫번째 단계에서는 $\phi$를 1로 정하고, Small Grid Search를 반영해 가장 좋은 정확도를 보이는 $\alpha, \beta, \gamma$의 초기값을 찾아낸다.
- 그 결과, $\alpha=1.2, \ \beta=1.1, \ \gamma=1.15$라는 초기값을 찾아냈으며, 이들을 고정한 뒤 $\phi$값을 증가시켜 3가지 요소를 모두 조절한다.
이러한 방식으로 $\alpha, \beta, \gamma$의 초기값을 정하고, $\phi$라는 독립변수를 통해 3가지 요소들을 모두 조절하는 것이 논문에서 제시하는 Compound Scaling이다.
4-3.EfficientNet-B0(BaseModel)
논문의 저자인 Mingxing Tan은 이전에 MnasNet이라는 모델을 이전에 발표했었는데, 해당 연구에 사용했던 구조와 파라미터들과 AutoML을 활용해 EfficientNet-B0 라는 모델을 찾게 되었다.
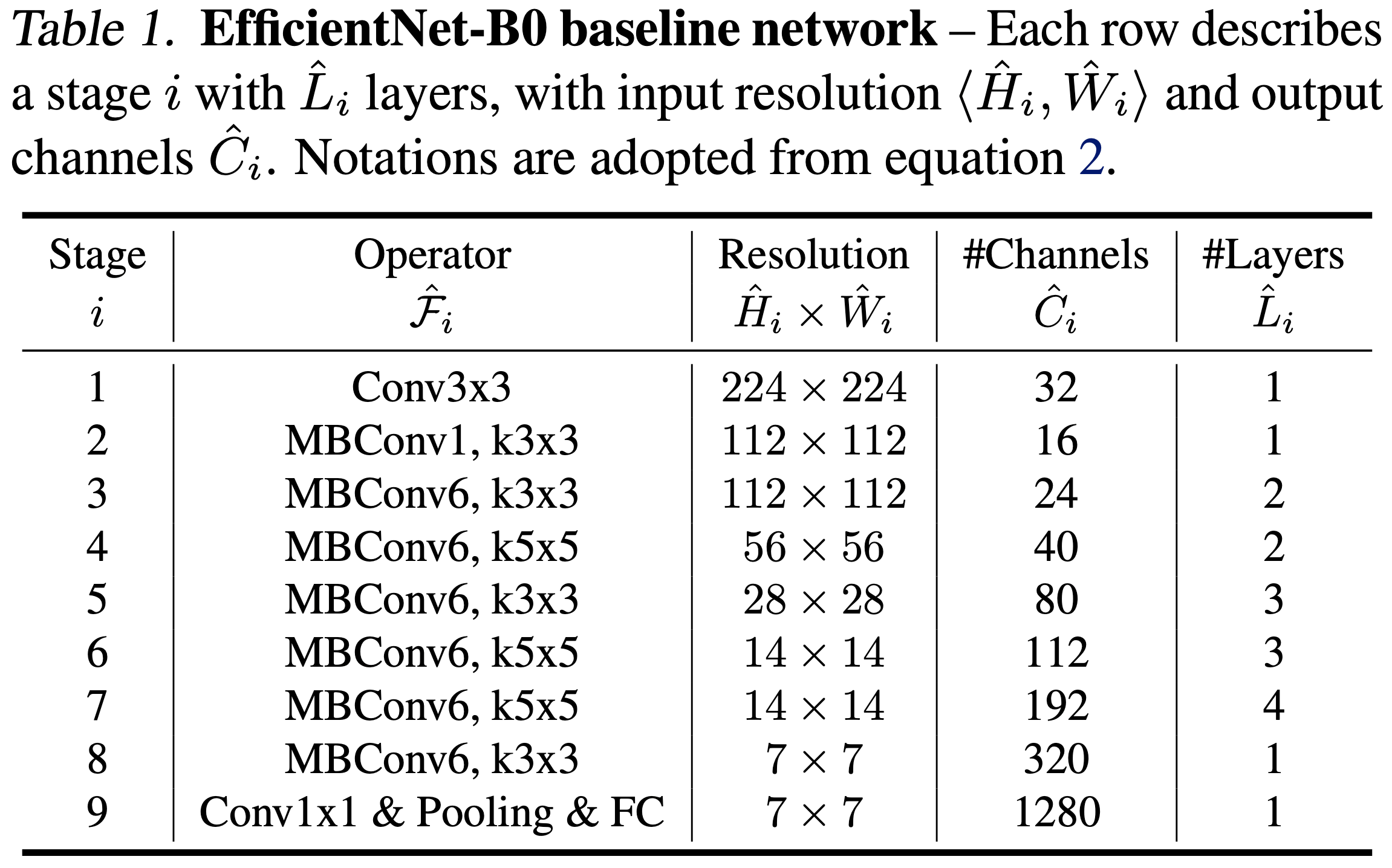
MBConv
EfficientNet-B0를 구성하는 MBConv Block의 구성은 다음과 같이 정리할 수 있다.
- Activation Function을 ReLU6에서
SiLU로 변경. - Pointwise convolution($1\times 1$ conv)을 통해 입력의 채널 수를 확장(Expand)시킨다.
- Depthwise convolution을 통해 확장된 입력의 채널별로 convolution filter를 적용한다.
- Squezze & Excitation이라는 연산을 통해 feature map을 압축하고, feature map의 각 채널에 가중치들을 곱한다.
- Pointwise convolution을 통해 확장되었던 채널의 수를 다시 줄인다.
- Drop Connect라는 것을 이용해 과적합을 방지한다.
- MBConv block의 입력과 Drop Connect의 출력간 skip connection을 적용한다.
SiLU

SiLU는 Sigmoid Linear Unit의 줄임말로 sigmoid 함수의 출력값에 입력값 $x$를 곱하는 연산을 수행한다.
이전에 봤던 다른 함수들은 입력에 따른 출력이 결정되어 있지만, SiLU는 입력 $x$를 곱하는 연산으로 인해 출력이 자체적으로 스케일링 되는 효과가 있다.
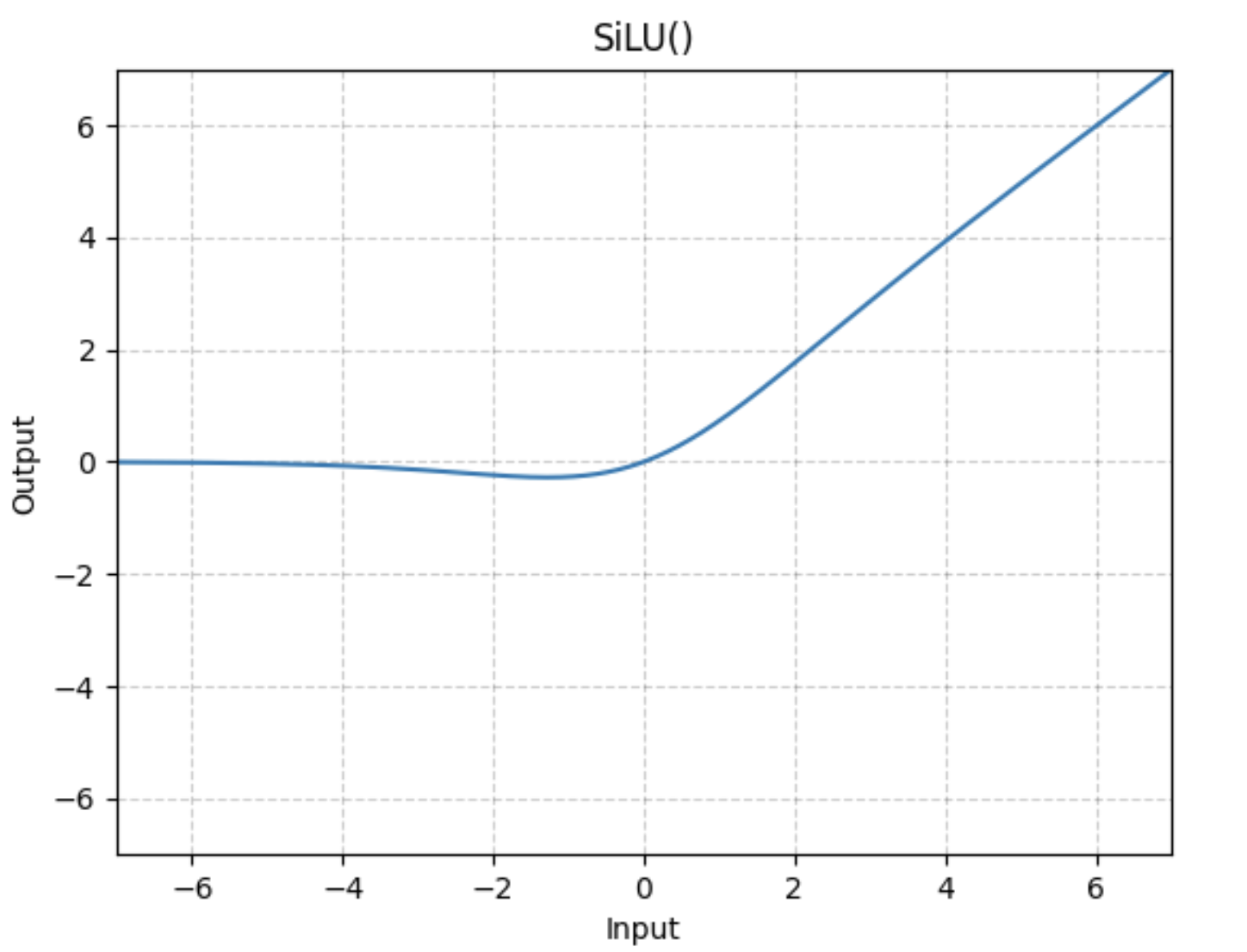
SiLU 함수의 그래프를 보면, SiLU는 어느 정도 작은 음수값에 대해서 허용하고, 절댓값이 큰 음수 입력은 0으로 만드는 것처럼 보인다. 하지만 정확하게는 모든 구간에서 미분이 가능하다.
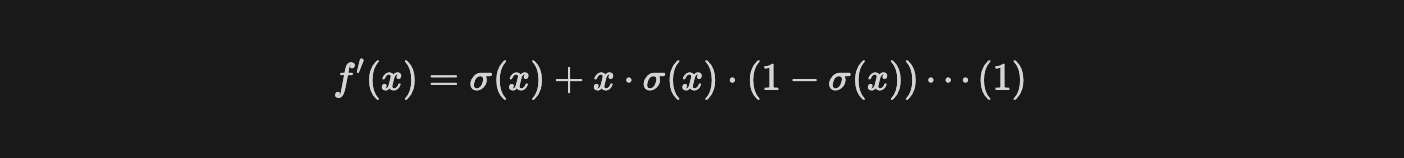
입력 $x$가 절댓값이 큰 음수라고 가정해보자.
식(1)에서 $\sigma(x)$는 0에 근사하는 양수이고, $1-\sigma(x)$는 1에 근사하는 값이다.
따라서 덧셈을 기준으로 두번째 항 $x \cdot \sigma(x) \cdot(1- \sigma(x))$은 $x\cdot \sigma(x) \approx 0$이고, $1-\sigma(x)$는 1에 근사하는 값이므로 두 값의 곱은 0에 근사하는 값이 된다.
근사하는 값이기 때문에 0이 아니며, 아주 작지만 기울기가 존재한다는 것이므로 모든 구간에서 기울기(gradient)가 발생할 수 있다.
결과적으로 SiLU 함수는 ReLU와 같은 다른 함수에 비해 모델의 수렴이 부드럽게 이루어지도록 돕는다.
Squeeze and Excitation
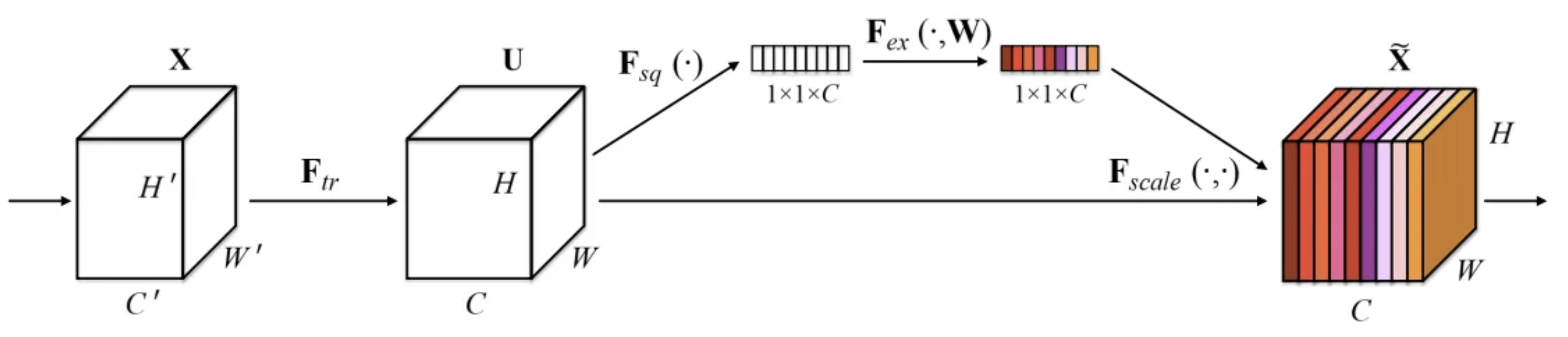
Squeeze and Excitation은 고차원의 feature map에서 각 채널마다의 가중치를 동적으로 조정해 중요한 특징은 더 강조하고, 덜 중요한 특징은 억제하는 알고리즘이다.
- Squeeze : Global Average Pooling을 사용해 각 채널에 대해 전체 공간적 차원의 평균을 구해 채널별 하나의 스칼라 값을 만든다. 결과적으로 각 채널을 대표하는 스칼라값들이 모여 하나의 벡터를 형성한다.
- Excitation : 두 개의 fully connected layer를 이용하는데, 첫번째 층(+ReLU)은 차원을 축소 시키고, 두번째 층(+Sigmoid)은 원래의 차원으로 복원한다. 첫번째 층의 축소를 통해 벡터의 원소들간 상관관계를 학습하도록 하며, 두번째 층에서 다시 원래 차원으로 복원함과 동시에 0과 1사이 값으로 인코딩해 각 채널의 중요도, 가중치를 나타낸다.
- 가중치 벡터를 SE block의 입력에 곱해줌으로써 각 채널의 중요도를 조정한다.
결과적으로 더 중요한 특징이 무엇인지 학습을 통해 파악하고, 이를 더욱 강조하는 형태가 되므로 학습의 수렴 속도와 모델의 정확도가 훨씬 높아지는데 기여하는 것이다.
Drop Connect
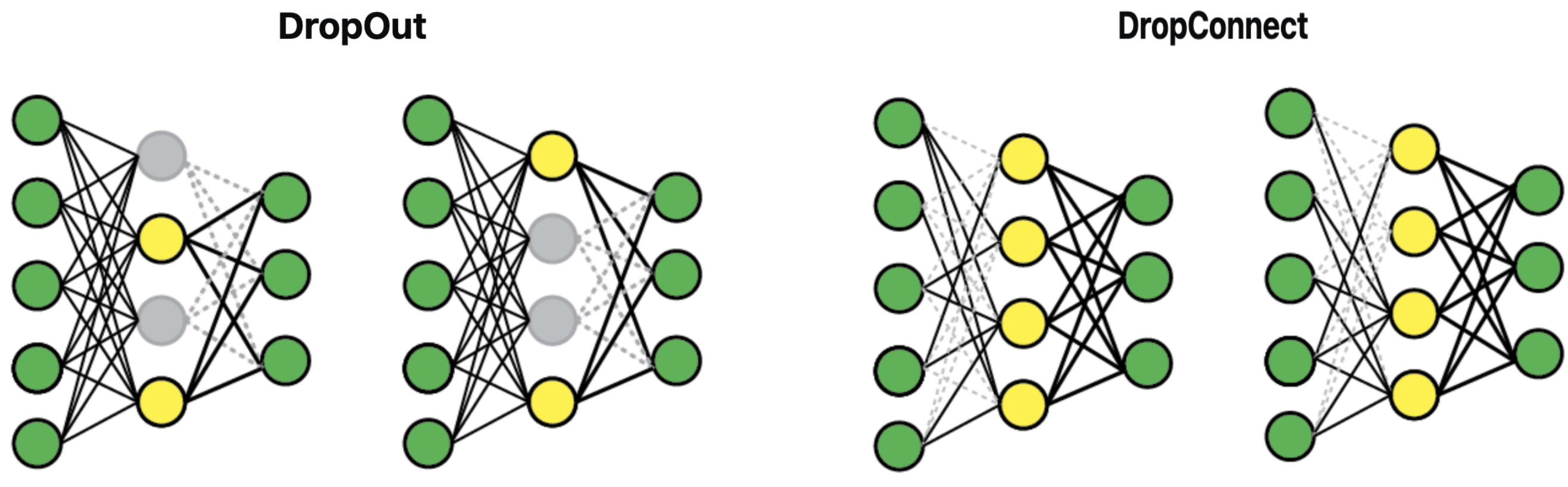
Drop connect는 Dropout과 같이 어떤 특성에 편향되는 것을 방지하기 위해 사용하며, 연결의 일부를 끊는다는 공통점이 있지만 대상이 다르다.
- Dropout은 무작위로 선택된 뉴런의 활성화 값을 0으로 설정 중 일부를 0으로 만든다.
- Drop connect는 가중치 행렬의 원소들 중 무작위로 선정한 일부(즉, 유닛들 중 일부)를 0으로 만든다.
별다른 차이가 없어보이지만, Dropout은 활성화된 출력값에 직접적으로 영향을 주는 반면, Drop Connect는 일부 임의의 가중치를 0으로 만들어 출력값에 간접적으로 영향을 주는 형태다.
따라서 Dropout은 특정 유닛의 출력을 제거해 이후 연결된 모든 유닛에 영향을 주게 되고, Drop Connect는 현재 layer에서 특정 유닛과의 연결을 제거해 이후 연결된 유닛들에 미치는 영향을 더 세밀하게 조절한다.
댓글남기기